Image Generation 정리(1)
## GAN [NIPS 2015]
https://bigdata-analyst.tistory.com/264?category=883085
Generative Adversarial Nets(GAN)
원 논문 arxiv.org/pdf/1406.2661.pdf 참고 자료 www.youtube.com/watch?v=AVvlDmhHgC4 나동빈님의 유튜브를 참고하여 진행하였는데 정말 갓동빈님이시다...설명을 이렇게 쉽게 해주시는 분은 거의 처음본다..역시.
bigdata-analyst.tistory.com
https://arxiv.org/abs/1406.2661
GAN은 Generator와 Discriminator로 서로 다른 2개의 network로 이뤄지고 이 두 network를 adverarial 하게 학습시켜 목적을 이루는 것.
Generator의 목적은 진짜 분포에 가까운 가짜 분포를 생성하는 것이 목적이고, Discriminator는 이 이미지가 가짜분포인지 진짜 분포인기 판단하는 것이다.
주어진 표본이 실제 표본이 될 확률이 0.5에 가까운 값을 가질 때 까지 계속 학습을 하는 것이다. 여기서 Fake로 확신하는 경우 discriminator의 확률 값은 0이 되고 실제로 확신하는 경우 판별기의 확률값이 1을 나타내게 한다. 따라서 판별기의 확률 값이 0.5인 것은 가짜인지 진짜인지 구분이 안된다라는 것을 의미
GAN의 목적함수

여기서 D는 Discriminator, G는 Generator. x는 실제 데이터를 의미, 가짜 데이터는 G(z)
D의 관점에서 실제데이터 x를 입력하면 D(x) 값이 커지면서 높은 확률값이 나오게 하고 가짜 데이터 G(z)를 입력하면 log 값이 점점 작아지게 만드는 것.
G 에서는 zero-mean gaussian distribution에서 noise z를 MLP에 통과시켜 샘플들을 생성하며 이 생성된 가짜 데이터 G(z)를 D로 넣었을 때 실제 데이터 처럼 확률이 높게 나오도록 학습된다.
즉 이 목적함수에서 1-D(G(z))을 높게 만들어서 전체적인 확률 값이 낮아지도록 하는 것으로 이는 G가 D가 잘 구분하지 못하는 데이터를 생성하는 것이 목적이다.

## Conditional GAN (cGAN) [2014]
https://arxiv.org/abs/1411.1784
GAN은 unsupervised learning으로 training dataset이 labeling 되어 있을 필요가 없다. 또한, Ranom 클래스 중에서 sample을 추출하는 것이다. 즉, 이는 unconditional 이라고 부른다.
conditional은 사용자가 직접 생성되는 이미지를 control 가능한 것이고, unconditional은 학습된 데이터셋에서 random하게 생성하는 것으로 사용자가 control 할 수 없다.
즉, 이를 MNIST dataset으로 예를 들면 1이라는 label 값을 주면 1이라는 이미지가 출력이 되는 것이다.
이에 대한 목적함수는 GAN 목적함수에 label 값 y를 조건부 확률로 주는 것이다.


## Unsupervised Representation Learning with Deep Convolution Generative Adversarial Networks (DCGAN) [ICLR 2016]
https://arxiv.org/abs/1511.06434
안정적인 훈련을 가능하게 하는 convolutional GAN의 구조를 제안하여 convolution을 사용한 GAN의 시초
학습된 discriminator를 사용하여 image classification task를 수행한다. DCGAN에서는 Generator에 초점을 맞춰서 서술. Discriminator는 pre-trained된 것을 사용
spatial pooling 함수를 strided convolution 으로 대체하는 모든 convolution network는 network가 고유의 spatial downsampling을 학습할 수 있도록 한다. 이는 DCGAN에서 Generator와 Discriminator 모두에 적용한다.
그리고 convolution feature의 가장 위에 있는 FC layer를 제거한다. 이는 Global average pooling은 모델의 안정성을 높이지만 수렴 속도에 안좋은 영향을 미친다. 따라서 Convolution feature들을 각각 Generator와 Discriminator의 입력과 출력으로 연결하는 것이 좋은 성능을 냄.
마지막으로 입력을 zero-mean과 unit variance를 가지도록 하는 각각의 unit으로 normalization 함으로써 Batch normalization으로 학습을 안정화 한다.
안정적인 Deep Convolution GAN을 위한 가이드라인은
- Generator에선 Pooling layer들을 strided convolution으로 대체하고, Discriminator에선 fractional strided convolution으로 대체한다. ※Fractional strided convolution = Transposed Convolution
- Generator와 Discriminator 둘 다 batch normalization 사용
- Fully connected hidden layer 제거
- Generator의 모든 layer에 ReLU 사용하고 output layer에만 Tanh activation function 사용
- Discriminator의 모든 layer에 Leaky ReLU activation function 사용

## InfoGAN : Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets [NIPS 2016]
https://arxiv.org/pdf/1606.03657.pdf
Entropy와 Mutual Information (상호정보량) 이라는 information theory 에서 사용하는 개념을 GAN에 반영하여 Unsupervised Learning 만으로도 데이터의 특징을 적절하게 표현할 수 있다.
기존 GAN의 문제점은 noise의 분포가 entangled(꼬여있다)하다는 것이다.

이러한 noise를 unsupervised-learning으로 distangled 하게 바꾸면 매우 효율적인 학습이 된다.
infoGAN은 GAN loss에 추가적인 항을 덧붙이는 방식을 사용하였다. noise를 GAN에서 사용되는 noise \(z\)와 latent code라는 데이터의 분포에서 중요한 값들을 표현하는데 사용하는 noise \(c\)로 두개의 값으로 구분한다. unsupervised learning으로 data의 distribution을 표현하겠다는 것은 \(c\)를 unsupervised learning으로 학습시키겠다라는 말과 동치이다. 그러나 GAN에서 \(z\)와 \(c\)를 함께 주기만 하는 것은 noise가 늘어나는 것에 불과하다.
이를 해결하기 위해 Mutual Information 개념이다. X와 Y의 mutual information은 I(X,Y)라고 표현하며 이는 Y를 알 때 X의 불확실성이 얼마나 감소하는가를 나타낸다. 이에 대한 정의는 다음의 식과 같다.
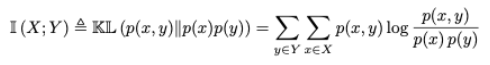
이를 conditional entropy로 나타내면
$$ I(X,Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) $$ 로 나타내지고 이를 집합개념의 도식화로 보면 다음과 같다.
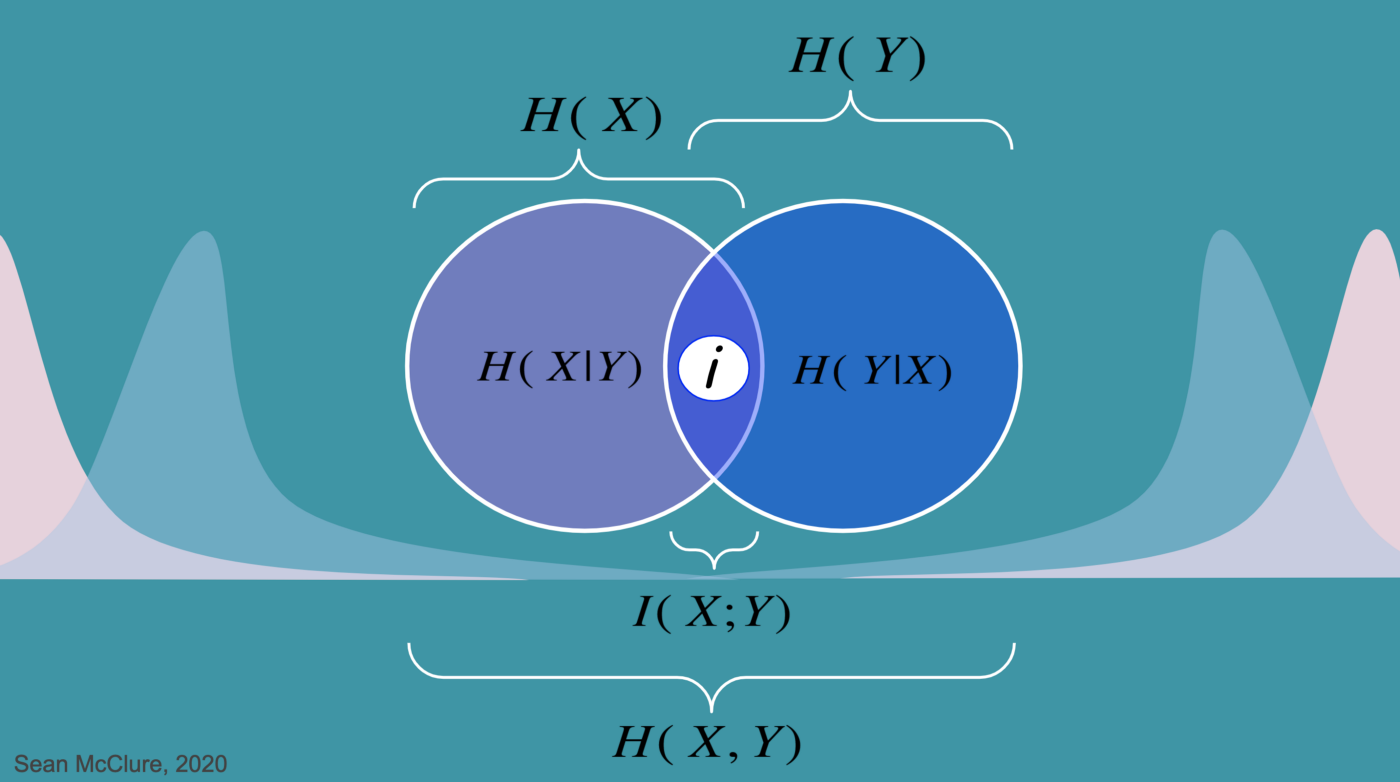
이러한 mutual information는 둘 중 하나의 변수를 관측함으로써 감소하는 나머지 변수에 대한 불확실성의 양이라는 관점로 볼 수 있다. 두 변수가 independent 하면 mutual information은 0이 되고, 두 변수가 하나의 변수가 다른 변수에 의해 완벽하게 설명되는 가역변수라면 최대가 될 것 이다.
이러한 Mutual Information theory를 적용하여 InfoGAN Loss function은 다음과 같다.
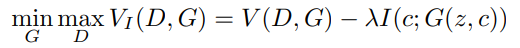
여기서 V(D,G)는 일반 GAN loss이다. 이는 GAN loss에 Regularization 항을 추가한 것으로 볼 수 있다. 이는 G(z,c)에 대해 P(c|x)가 작은 entropy를 갖는 것을 원하는 것이고 즉, I(c;G(z,c))가 maximize하는 방향으로 Generator가 학습되길 원하는 것이다. 왜냐하면 c는 distribution의 semantic feature이기 때문에 Generator가 semantic하게 학습이 되길 원하고 이는 불확실한 양을 최대한 줄이기 위함 즉, 각 분포들이 semantic 하게 되어 distribution이 distangle하게 만들기 위함이다.
하지만 이 과정에서 P(c|x)를 알아야지 mutual information을 구할 수 있다. 이는 infoGan 에서는 임의의 분포 Q(c|x)를 이용하여 \( L_{I}(G,Q)\)를 I(c;G(z,c))의 하한선이 되게 한다. 이에 따른 수학적 근거는 Variational Information Maximization 이다. 다시 한 번 말하면 I(c;G(z,c))를 최대화하는 것이 아니라 그것의 하한인 \( L_{I}(G,Q)\)를 최대화하면 P(c|x)를 모르는 문제를 해결할 수 있다.
따라서 InfoGAN의 최종적인 loss는 다음과 같이 쓰일 수 있다.
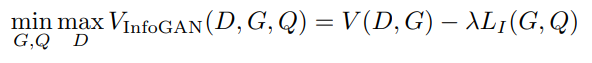
## Image-to-Image Translation with Conditional Adversarial Networks(Pix2Pix) [CVPR2017]
https://arxiv.org/abs/1611.07004
pix2pix는 image-to-image translation 모델이다. 이 논문은 translation problems을 위한 일반적인 framework를 개발하는데 초점을 맞추었다.
pix2pix는 Ground Truth 값이 존재하고 픽셀마다 annotation이 되어야한다는 전제를 설정하고 진행한다.
pix2pix는 비유적인 표현을 통해 원하는 목적성을 말하면서 설명한다.
먼저 L1 Loss를 사용하여 CNN의 예측값과 실제값의 Euclidean distance를 최소화 하는 방향으로 학습을 한다. 그러면 결과가 blurring의 효과를 가지게 된다. 이는 generator가 어느 것을 택해도 loss가 너무 커지지 않도록 중간의 어떤 애매한 것을 택하는 경향 때문에 Average 학습이 되어버리게 된다.
다음으로 생성된 이미지가 좀 더 실제 같길 원하는 요청사항을 준다. 이는 GAN과 같은 원리이고 단순 GAN이 아닌 cGAN을 사용한다. 이는 conditonal 이라는 개념에 초점을 맞추어 유저가 control 할 수 있는 Generation을 원하기 때문에 cGAN loss를 사용한다. cGAN loss에서 label인 y에 inpt image를 넣어준다. 이 말은 즉, input 이미지와 연관된 이미지를 생성하는 목적을 가짐을 의미한다.
따라서 pix2pix는 1. 실제값과 예측값의 euclidean distance가 최소화 되길 원한다. 2. 생성된 이미지가 실제값과 같길 원한다. 라는 2가지 요청사항을 모두 만족하는 최종적인 loss function을 개발한다.( 사실 그냥 더하는거)
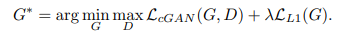
cGAN loss와 L1Loss를 더하는 이유는 아무리 cGAN이 input x를 참고한다 하더라도 generator는 오직 D를 속이는 것에 초점을 맞추기 때문에 input x가 덜 반영될 수 있기 때문이다. 따라서 이미지 G(x,z)와 대응되는 y 이미지를 직접 비교하는 L1 Loss를 추가한다.
Generator는 U-Net의 기본구조를 따르고 Encoder-Decoder 구조에 skip connection을 추가하여 decoder가 학습이 잘 되지 않는 문제를 해결한다.
Discriminator는 Patch-GAN의 Discriminator 구조를 따른다. Patch GAN의 원리는 이미지를 N x N의 크기를 가지는 Patch 로 나누고 그 각각의 Patch에 대해 참/거짓을 판별한 뒤 voting 형식으로 참/거짓을 분류한다. 이는 더 locality feature가 많이 반영되는 방식이므로 high-frequency를 구분하는데 좋다.
## WassersteinGAN (WGAN) [PMLR2017]
https://arxiv.org/abs/1701.07875
Unsupervised learning은 training data x 에 대한 label y가 없는 상태에서 데이터 x의 distribution P(x)를 직접 학습하는 방법으로 이를 위해 다음과 같이 표현이 된다.
$$ max_{\theta \in \mathbb{R}^{d} } \frac{1}{m} \sum^{m}_{i=1} log P_{\theta} (x^{(i)})$$
그러나 P(x)를 표현 하는 것은 어렵기 때문에 GAN에선 latent variable z의 분포를 가정하여 입력하고 generator의 분포를 P(x)에 가깝게 학습시키고자 한다. 그러나 이는 discriminator와 generator간의 균형을 유지하며 학습하긴 어렵고, 학습이 완료된 후에도 mode collapsing이 발생한다. 이는 discriminator가 역할을 제대로 수행하지 못하여서 생긴 문제이다.
따라서 WGAN은 다음과 같은 contribution으로 이러한 문제를 해결하고자 한다.
- discirminator 대신 새로 정의한 critic을 사용한다. discriminator는 fake/real 를 판단하기 위해 sigmoid 를 사용하고 output은 fake/real 에 대한 probability이다. 반면에 본 논문에서 제안한 critic은 EM(Earth Mover) distance로 부터 얻은 scalar 값을 이용한다.
- EM distance는 probability distribution의 거리를 측정하는 척도 중 하나이다.
※ mode collapsing 이란?
Generator가 다양한 이미지를 만들어내지 못하고 비슷한 이미지만 계속 생성하는 경우가 있다. 이를 Mode Collapsing 이라고 한다. 예를 들어 MNIST에서 0~9 까지의 숫자가 있을 때, 노이즈를 변환할 때 변환된 데이터 라벨 분포가 특정 숫자로 치우칠 때 Mode Collapsing이 되었다고 한다. 이러한 현상은 Discriminator가 완벽하지 못하거나 모델이 진동할 때 발생한다.
이 논문에서 4가지의 거리 종류를 설명한다. 간략하게 정리하기 위해서 평소 같으면 정리하지 않지만 새로운 insight를 얻기 위해 정리한다.
1. Total Variation(TV)
TV distance는 다음과 같은 식을 따른다.
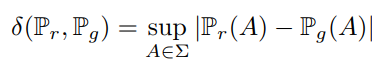
본 식은 두 확률 분포의 측정값이 벌어질 수 있는 가장 큰 값을 뜻한다. notation을 잠깐 보자면 \( \sup \)는 상한(supremum)을 말하고 상계 중 가장 작은 값을 말한다. 하나의 예시를 들어 [0,2) 라는 무한집합이 있을 때, 2는 집합에 포함되지 않지만 2보다 큰 실수는 없으므로 여기서 상한은 2이다.
즉, \( \mathbb{P}_{r}(A) \) 라는 확률 분포와 \( \mathbb{P}_{g}(A) \) 라는 확률 분포의 차이에서 가장 큰 값을 말하는 것이다. 같은 집합 A에 대해서 확률분포가 측정하는 값은 다를 수 있어서 모든 \( A \in \sum \)에 대해 가장 큰 값을 정의한 식이다.
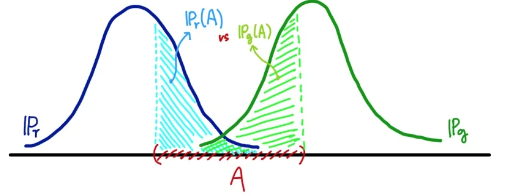
위 그림에서 알 수 있듯이 두 distribution의 교집합이 없으면 TV는 1이 된다.
2. Kullback-Leibler (KL) divergence
KLD는 GAN에서 사용하는 distance 지표이다. 정확하게 말하자면 KLD는 distance metric은 아니다. 삼각부등식과 교환법칙이 성립되지 않기 때문이다. KLD는 \( \mathbb{P}_{r}\) 분포와 \( \mathbb{P}_{g}\)의 분포가 얼마나 다른지 나타내준다.
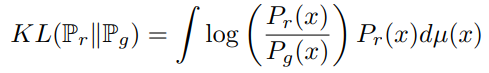
3. Jensen-Shannon divergence
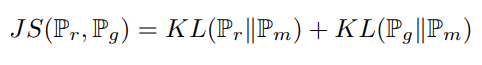
여기서 \( \mathbb{P}_{m} \)은 median 값으로 \( \frac{1}{2} (\mathbb{P}_{r}+\mathbb{P}_{g}) \) 이다. JSD는 KL과 달리 distance metric으로 활용될 수 있다. 당연하지만 \( \mathbb{P}_{r} = \mathbb{P}_{g}) \)이면 JSD는 0이다.
4. Earth-Mover (EM) distance == Wasserstein distance-1
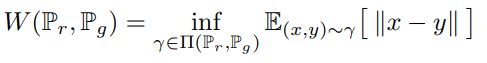
위 식에서 \( \Pi ( \mathbb{P}_{r} , \mathbb{P}_{g} \)는 두 확률 분포 \( \mathbb{P}_{r} , \mathbb{P}_{g} \)의 결합확률분포 (joint distribution)들을 모은 집합이고 \( \gamma \)는 이 결합확률분포의 원소 중 하나이다. 따라서 위 식은 모든 결합확률분포 \( \Pi ( \mathbb{P}_{r} , \mathbb{P}_{g} \) 중에서 ||x-y||의 기대값을 가장 작게 추정한 값을 의미한다. 이 때 ||x-y||는 euclidean distance이다.
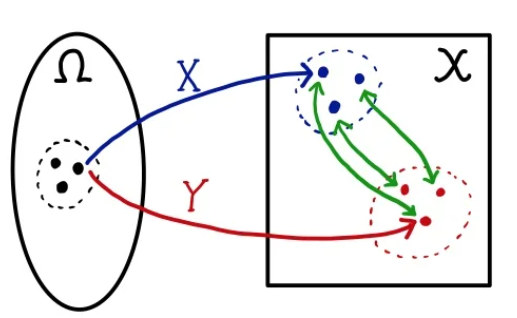
이를 좀 더 풀어서 설명하자면, \( w \) 값을 하나 sampling 하면 두 점 \( P_{r}(w)\)와 \( P_{g}(w)\) 간의 거리를 구할 수 있다. 이러한 sampling을 반복하면 결합 확률 분포 \( \gamma \)의 윤곽이 들어나고 이는 주변확률분포가 생성된다. 여기서 X와 Y가 분포하는 모양은 변하지 않지만 경향이 w가 뽑히는 순서에 따라 경향이 달라질 순 있다. 그래서 이에 대한 기대값을 구하여 기대값이 가장 작게 나오는 확률분포를 취하는 것이 Wasserstein distance이다.
이러한 Wasserstein distance는 다음과 같은 부등식을 만족한다.
$$ ||X,Y|| = ( | \theta - 0| ^{2} + |Z_{1}(w) - Z_{2}(w)| )^{\frac{1}{2}} \geq | \theta | $$
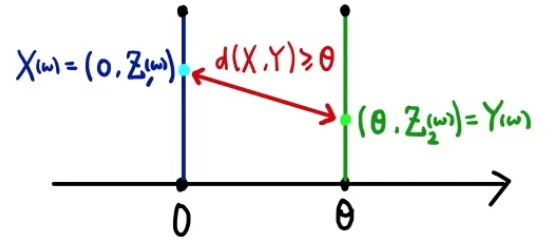
즉, 이 식은 ||X,Y||의 기대값은 어떤 결합확률분포 \( \gamma \)를 사용하든 항상 \(| \theta | \)보다 크거나 같다. \( || X,Y|| == | \theta| \) 인 경우는 \( Z_{1} = Z_{2} \) 이다.
본 거리들을 정리하자면 TV, KL, JS는 \( \mathbb{P}_r \), \( \mathbb{P}_g \)가 겹치지 않는 상황에서는 불연속이된다. 반면에 Wasserstein distance는 TV, KL, JS 보다 weak metric으로 수렴을 판단하는게 soft하다. 이는 분포 수렴과 동일하다. 분포수렴은 제일 약한 수렴으로 확률분포의 개별적인 특징보다 전체적인 모양을 중시하는 수렴이다. 중심극한정리에 의해 표본 평균이 정규분포로 수렴하는 종류가 분포수렴이다.
분포수렴하는 조건은
1. \( X_{n} \)의 모든 모멘트가 X의 모멘트로 수렴
2. \( X_{n} \)의 누적확률밀도함수가 X의 누적확률밀도함수 중 연속인 모든 점에서 수렴
3. \( X_{n} \)의 Fourier transform이 수렴
따라서 Wasserstein distance는 분포가 겹치던 안겹치던 최소 \( | \theta |) 가 유지되므로 학습에 사용하기 쉽다.
Wasserstein distance는 inf 부분은 계산하지 못하고 \( \mathbb{P}_{r} \)은 알고있는 대상이기 때문에 이를 바로 loss로 바로 사용할 수 없다. 또한, 미분도 불가능하다. 따라서 이를 Loss function으로 바로 사용하지 못하기 때문에 약간의 수식 변환이 있어야 한다.
Kantorovich-Rubinstein duality를 이용해 식을 변환하면
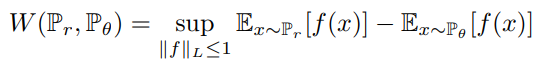
다음과 같은 식이되고 여기서 이를 학습시키기 위해 parameter가 추가된 f로 수식을 바꾸고 \(\mathbb{P}_{\theta} \)를 \(g(\theta)\)에 대한 식으로 바꾸면
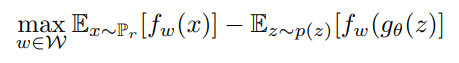
다음과 같은 식이 된다. 위 식에서 \(\mathbb{P}_{r} \)은 update(미분)할 때 사라짐으로 큰 신경을 안써도 된다.
또한, 1-Lipschitz 조건을 만족시키기 위해 weight-clipping을 해준다. (이는 clearly terrible way라고 논문에서 언급한다.)
※ weight clipping (Gradient Clipping) : graident vector의 방향은 유지하되 그 크기는 학습이 망가지지 않을 정도로 norm의 크기를 제한하는 방법
GAN과 WGAN의 loss 비교는 다음과 같다.

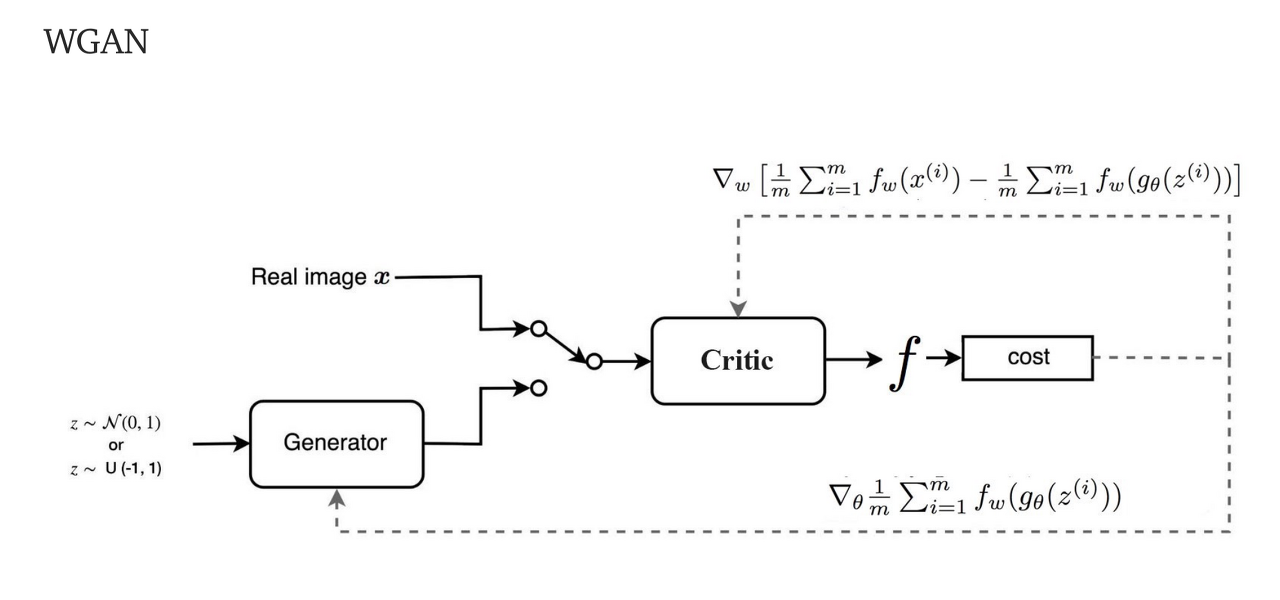
※ WGAN에 대한 자세한 설명은 추후 정리한다.
## Improved Training of WassersteinGAN (WGAN-GP) [NIPS2017]
https://arxiv.org/pdf/1704.00028.pdf
WGAN의 문제점은 Lipschitz constraint를 부과하기 위해 weight clipping을 사용하여 안좋은 샘플들의 생성과 수렴의 실패로 이어지는 것이다. 따라서 WGAN-GP는 weight clipping 방법이 아니라 gradient의 norm에 패널티를 부과하는 방식을 제안한다. 이로써 WGAN 보다 좋은 성능을 보이고 학습의 안정화를 이뤄냈다. 따라서 본 모델이 WGAN-GP 인 이유는 뒤에 GP가 Gradient penalty이다.
따라서 WGAN-GP는 다음과 같은 Loss function을 가진다.
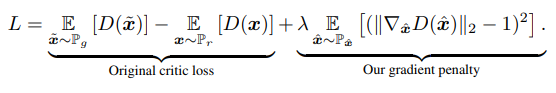
미분 가능한 함수 f는 1-립스키를 만족하고 모든 곳에서 norm이 최대 1인 기울기가 있는 경우에만 가능하다. 이를 기반으로 실제 데이터와 생성된 데이터 사이에 보간된 점은 f에 대해 1의 gradient norm을 가져야한다. 따라서 cliping을 적용하는 대신 graident norm이 1과 멀어지게 되면 모델에 penalty를 줘서 1에 가깝게 만드는 것이다. 여기서 \( \lambda =10 \)으로 설정한다.
WGAN-GP는 또한, Discriminator의 batch normalzation을 사용하지 않고 layer normalization을 사용한다.
#### Reference
https://ysbsb.github.io/gan/2020/06/17/GAN-newbie-guide.html
딥러닝 GAN 튜토리얼 - 시작부터 최신 트렌드까지 GAN 논문 순서 | mocha's machine learning
이번 포스팅에서는 GAN의 개념, GAN의 종류, 주요 논문들에 대한 짧은 리뷰를 이야기하려고 합니다. GAN의 종류들은 중요하게 언급되는 모델들을 선정하였고, 이 모델들에 대해서 간단히 설명을 듣
ysbsb.github.io
https://pseudo-lab.github.io/Tutorial-Book/chapters/GAN/Ch1-Introduction.html
1. GAN 소개 — PseudoLab Tutorial Book
개요 (Overview) GAN은 Generative Adversarial Networks의 약자로 우리말로는 “적대적 생성 신경망”이라고 번역되는 AI기술 중 하나입니다. GAN은 실제에 가까운 이미지나 사람이 쓴 것과 같은 글 등 여러
pseudo-lab.github.io
https://kangbk0120.github.io/articles/2017-08/info-gan
InfoGAN Review
Review: Info GAN 강병규 안녕하세요. GAN의 다양한 논문들을 계속 리뷰해오고 있는데 이번에는 Info GAN에 대해서 한번 리뷰해보고자 합니다. 먼저 이 논문에서 주장하는 기존 GAN 문제점들에 대해서 알
kangbk0120.github.io
https://di-bigdata-study.tistory.com/8
[pix2pix] Image-to-Image Translation with Conditional Adversarial Networks 논문 정리
이번에 정리해볼 논문은 pix2pix 모델을 설명하고 있는 Image-to-mage Translation with Conditional Adversarial Networks 논문이다. 사실 Cycle GAN 논문을 정리하다보니, 이 pix2pix 논문을 한번 읽고 넘어가면..
di-bigdata-study.tistory.com
https://www.slideshare.net/ssuser7e10e4/wasserstein-gan-i
Wasserstein GAN 수학 이해하기 I
이 슬라이드는 Martin Arjovsky, Soumith Chintala, Léon Bottou 의 Wasserstein GAN (https://arxiv.org/abs/1701.07875v2) 논문 중 Example 1 을 해설하는 자료입니다
www.slideshare.net