Linear Regression
Linear Regression을 확률론적 관점으로 풀어본다. (PRML)
## Supervised Learning
Supervised Learning은 N개의 관측치 \( \{ x_1, \cdots , x_n \} \) 와 target value \( \{ t_1 , \cdots , t_N \} \) 와의 관계를 구하여서 새로운 x가 들어왔을 때 새로운 값 t를 예측하는 것이다.
이를 구하기 위해선 가잔 간단한 방법으로는 x와 t와의 관계를 함수 y(x) 로 나타내어 새로운 t를 예측하는 것이다.
그리고 또 다른 방법으로는 확률론적 관점을 통해 보며 예측 분포 \( p (t|x) \) 를 modeling 하는 것이다.
따라서 본 포스팅에선 이 두가지 방법을 이용하여 Linear Regression을 설명해보겠다.
## Linear Regression

이러한 Regression 식은 다음과 같이 표현이 된다.
$$ Y = mX + b $$
여기서 Y는 Reponse Variable 즉, 반응변수 = 종속변수 이고, m은 slope , X는 covariate, b는 bias로 intercept이다.
이런 식으로 간단하게 1차 선형 모델을 구축할 수 있다.
그러면 왜 우리는 처음으로 공부할 때 Linear regression model을 배울까?
이에 대한 이유는 4가지 정도로 있다. 첫번째로 매우 널리 쓰이는 모델이라는 점이다. 그리고 두번째로는 큰 모델의 기본이 된다는 것이다. 3번째와 4번째가 가장 중요한데 해석이 쉽고, 풀기가 쉽다는 것이다. 따라서 이러한 단순성 때문에 Linear model을 사용한다.
그럼 Regression model에 대해 알아보자
비단 Regression model 뿐만은 아니지만 독립변수 x를 이용하여 종속변수 y를 예측하는 것이다.

위 그림을 간단히 설명하자면 independent variable(vector) x는 p 차원의 실수 범위 안에 있는 변수이다. 이를 통해 실수 범위에 있는 y(response variable) 를 예측하는 것이다.
이는 joint probability로도 설명이 된다. joint probability는 bayes' rule에 의해 다음의 식처럼 표현이 된다.
$$ p(x,y) = p(x) p(y|x) $$
여기서 독립변수 x를 condition으로 생각하여 x라는 사건이 발생했을 때의 y의 확률을 이용하는 것이다. 따라서 이러한 조건을 가지는 확률 p(y|x)는 discriminative model 이라고 부른다.
그러면 데이터가 1개가 아닌 여러개가 있을 때는 어떻게 표현할까
다시 data D에 대해 재정의한다. \( D = \{ (x_1 , y_1 ),\cdots , (x_n , y_n ) \} = \{ (x_i , y_i ) \}_{i=1}^{n}\) 처럼 data를 정의할 수 있다. data는 서로 independent 하고 서로 동일한 분포를 가진다. 이에 따른 palte diagram은
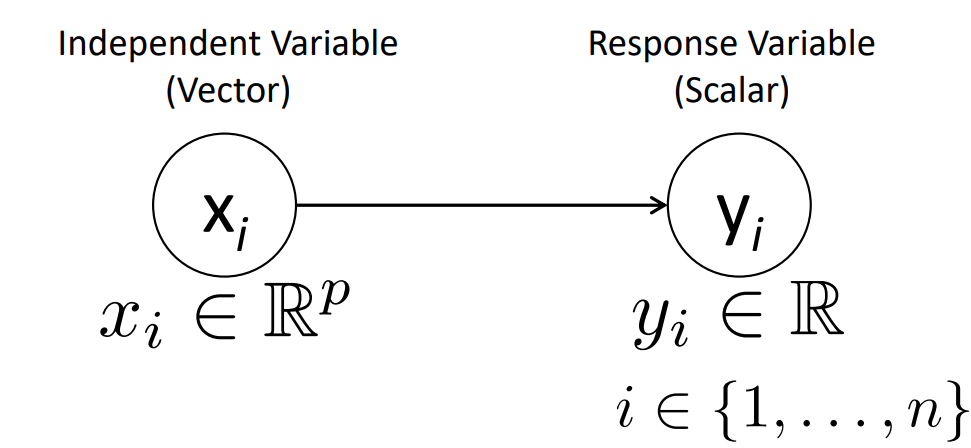
다음과 같이 나타나진다.
그래서 앞서 본 joint probability도 서로 independent 하기 때문에 곱으로 나타내지고
$$ p(D) = \Pi_{i=1}^{n} p (x_i , y_i ) = \Pi_{i=1}^{n} p (x_i ) p(y_i | x_i ) $$
와 같은 식으로 나타내진다.
이제 linear model에 대한 식에 대해 더 알아보자. 우리가 아는 1차 linear model은 y = Ax + b라고 간단하게 표현이 된다. 이제부턴 이를 모두 vector로 표현하여 p-dimension을 가진 식으로 다시 쓰면
$$ y = \theta^{T}x + \epsilon $$
다음과 같이 나타낸다. 이를 조금 풀어서 p=3 일 때를 가정해서 쓰면

이처럼 풀어진다.
이러한 식에 용어를 한 번 다시 정리하면
y : scalar response , \( \theta \) : vector of paramters , x : vector of covariates , \( \epsilon \) : noise
여기서 noise는 보통 normal distribution을 따른다고 가정한다. 따라서 이 식을 summation으로 나타내면
$$ y = \Sigma_{i=1}^{p} \theta_{i}x_i + \epsilon $$
처럼 된다.
이를 여러개의 데이터가 있는 matrix 처럼 표현하면 X와 Y는

이런식으로 구성이 된다. 위 식과 다르게 row의 개수는 data의 개수가 되고 column의 개수는 data의 차원이 된다. 따라서 nxp의 matrix가 된다. y는 vector 가 되어서 n x 1의 형태를 갖는다. 따라서 이러한 matrix 와 vector들을 그림으로 표현하면
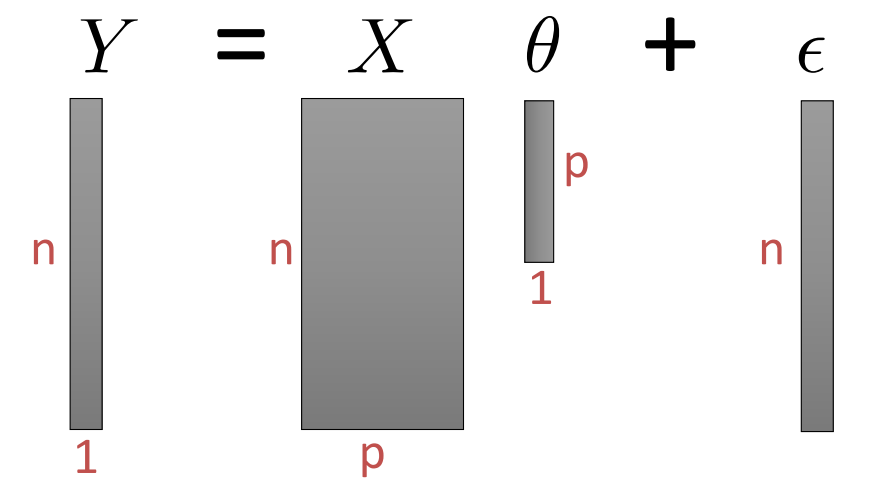
다음과 같이 그려진다.
그러면 여기서 한가지 드는 의문점은 bias는 어떻게 표현하는가이다.
bias는 \( \theta \)와 x 에 간단한 트릭으로 표현한다.
\( \theta = [ b, \theta_1 , theta_2, theta_3] \)로 표현하고 \( x = [1, x_1, x_2, x_3]^{T} \) 로 표현하면 bias를 표시할 수 있다. 이렇게 되면 단순 전개로 표현하면 \( b+ \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 \) 로 표현이 되어 bias를 vector 형태로 깔끔하게 표현할 수 있다.
이는 확률론적인 관점에서 보면 conditional likelihood 로 볼 수 있다.
Likelihood는 \( p(D| \theta) \) 로 표현되는 것을 그 전 포스팅에서 알아보았다. 여기서 Data D는 {x,y} 가 된다.
그러면 이를 다시 표현하면 \( p( \{ x,y \} | \theta ) \) 가 된다. 이를 condition 을 주어서 다시 표현하면 결국은 \( p(y| x, \theta ) \)가 된다. 따라서 x에 대한 condition이 주어졌을 때 y의 확률( p(x|y) )을 linear model에 기반하여 풀어보자
그러면 이를 어떻게 풀까? 다시 한 번 linear model 에 대한 식을 적어보겠다.
$$ y = \theta^{T} x + \epsilon $$
여기서 \( \epsilon \)은 앞서 언급했듯이 평균이 0인 normal distribution을 따른다고 하였다. 따라서 이 noise \( \epsilon \)이 key 가 된다. \( \theta^{T} x \)가 정해졌다고 하면 이는 constant로 고정된 하나의 상수가 된다. 그러면 Normal distribution + constant는 어떻게 될까? 바로 평균의 값이 옮겨지게 된다. 따라서 Y에 대한 값은 다음과 같은 분포를 따른다고 할 수 있다.
$$ Y \sim N (\theta^{T} x , \sigma^{2} ) $$
이렇게 평균이 \( \theta^{T} x \)인 Gaussian distribution을 따르므로 conditional likelihood는 다음의 식처럼 표현이 된다.

이렣게 likelihood의 식을 구했으니 이 식을 풀기 위해 \( \theta , \sigma \)를 구해야한다.
이를 구하기 위해 Bayesian 관점에 따르는 Posterior distribution에 대한 추정과 Frequentist 관점에서의 likelihood에 대한 추정을 한다.
우선 Baysian 관점에서의 conditional distribution y 를 생각하면
$$ p(y | x , \theta , \sigma^2 ) $$
여기서 \( \theta \)와 \( \sigma \)는 random variable로 어떠한 특정한 분포를 따르는 Priror distribution이라고 생각을 한다.
반면에 Frequentist는
$$ p_{\theta , \sigma^2} (y | x) $$
로 \( \theta \)와 \( \sigma \)를 고정된 값이라고 본다. 즉, \( \theta \)와 \( \sigma \)는 어떠한 분포를 따르지 않는다라고 생각한다.
그러면 이러한 방법을 이용해서 paramter를 구하는 방법에 대해 알아보자. 먼저 Frequentist 의 관점인 MLE로 구해보자
MLE에서는 \( Y = X \theta + \epsilon \) 에서 noise 부분을 상관하지 않고 \( \theta \)를 구하는 것을 집중해서 한다.
\( \theta \)를 구하는 방법은 두가지가 있다. 처음으로 기존에 했었던 Analytically 한 방법 즉, \( \theta \)에 대해서 미분을 하였을 때 0이 되는 지점을 구하는 것이다. 두번째로는 Iteratively 하게 gradient descent 방법을 이용한 것이다. gradient descent 방법에 대해 간단히 설명하자면 \( \theta^{*} = \theta_{old} + \Delta \theta \)이다. 즉, 기존의 \( \theta \) 값을 update 함으로써 최적의 \( \theta^{*} \) 값을 찾는 것이다.
먼저 likelihood를 구하기 위해 앞서 살펴본 식을 다시 한 번 보자.
$$ p(D) = \Pi_{i=1}^{n} p(x) p(y|x) $$
이는 joint probability 를 구하는 공식이다. 그런데 p(x) 즉, data에 대한 확률은 모두 동일하므로 1이 된다. 그래서 이는 없는 것으로 취급할 수 있다.
따라서 이런 성질을 이용하여 Likelihood를 구해보자.
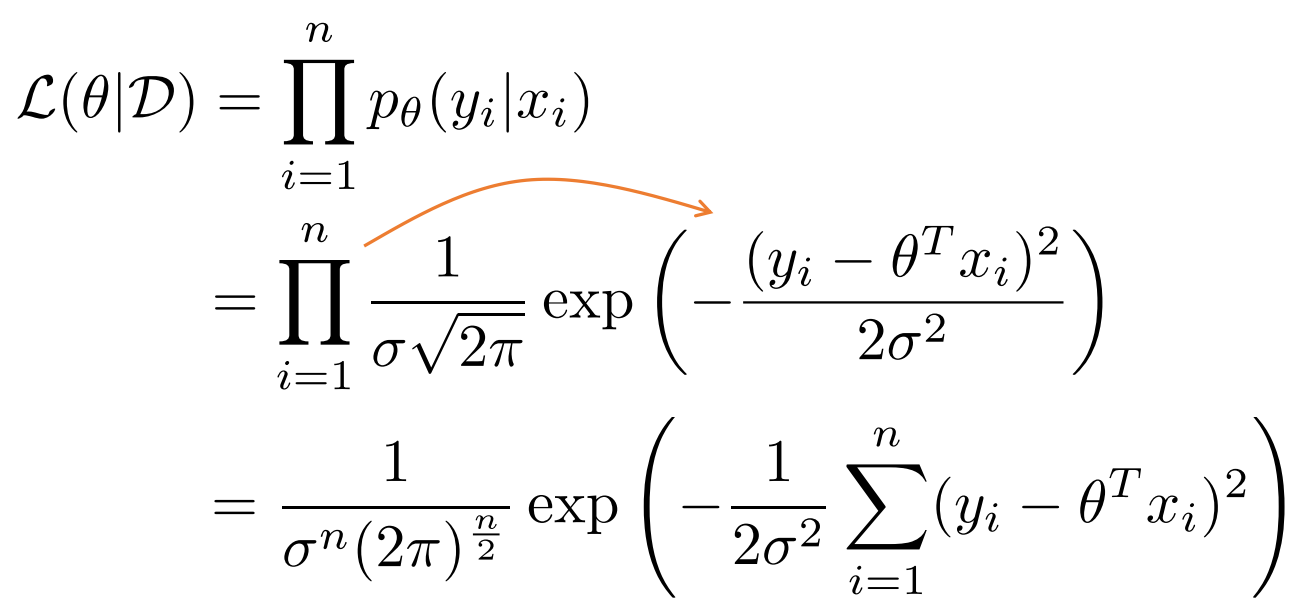
위에서 알아봤듯이 \( p_{\theta} (y | x) \) 를 대입해서 풀면 다음과 같이 나온다.
먼저 처음은 likelihood \( p(D|\theta) = p (\{ y_1 , \cdots , y_n \} | \{ x_1 , \cdots , x_n \} , \theta ) \)를 정리하여 나온 식이다.
따라서 위처럼 conditional likelihood를 구하였고 이제 parameter \( \theta \)를 구해보자
\( \hat{\theta_{MLE}} = argmax \ln L (\theta | D ) \)로 log를 취해줘서 구한다. 따라서 이를 반영한 식은

위와 같이 되고 여기서 우리는 최대화된 값이 아니라 어느 부분에서 최대화가 되는지를 알고싶으니 constant 부분을 무시하고 최적화하면 최종적으로

이런식으로 정리된다.
따라서 이를 다시금 정리하면

이렇게 나오게 되고 여기서 있는 마이너스를 제거하여 minimize로 바꿔

다음과 같은 식이 도출된다.
따라서 이는 제곱 에러를 최소화하는 것에 수렴하게 된다.
그러면 이렇게 얻은 제곱에러를 최소화 시켜서 어느 \( \theta \)에서 최소화가 되는지 알아보자
loss function을 보면 결국 2차 convex function이다. 이는 매우 간단하게 형태가 되어있으므로 미분했을 때 0인 값이 결국 극솟값이 된다. 따라서 \( \theta \)로 미분을 하여 0이 되는 값이 loss를 최소화 하는 값이 된다.
이를 전개하면
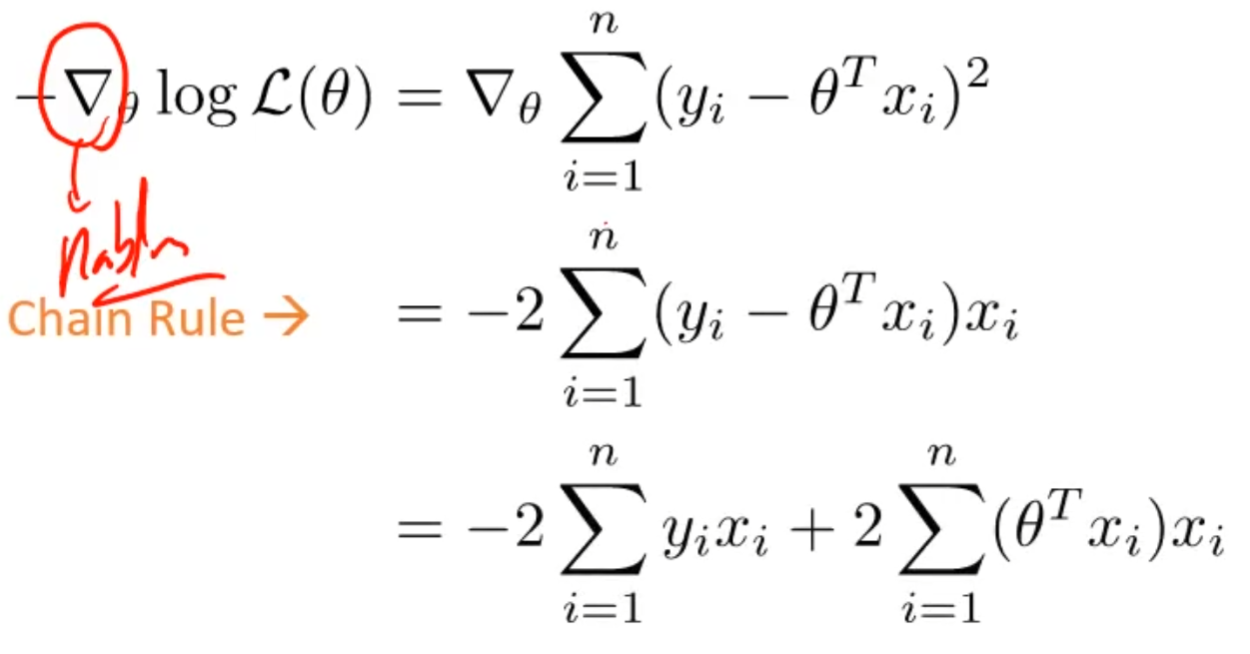
다음과 같이 도출이 된다. 이렇게 도출한 미분한 값을 matrix 형태로 표현하면
$$ -2X^{T}Y + 2X^{T}X \theta $$
가 된다.
이러한 행렬식을 hessian 방법을 통해 두번 미분한 값이 0보다 크거나 작으면 convex function임을 증명한다. (NLL 도 convex function임을 증명)

여튼 본론으로 돌아와서 이렇게 나타난 식 = 0 이라는 것을 풀어보면

다음과 같이 도출된다. (Linear algebra에서 많이 본 식이 나옴..)
이제 이를 linear algebra 관점으로 간단하게 봐보자
MLE의 목적은 결국 \( \hat{y} \)가 y 와 가까워지도록 하기 위한 것이다.

y가 x의 column space에 존재하지 않을 수 있으므로 최대한 y와의 거리를 줄이는 것이라고 생각하면 된다. (projection을 최소화) 따라서 y와 y hat의 차이는 y와의 거리가 수직임을 의미하고 \( X^T ( Y - \hat{Y} ) = X^T (Y - X \theta ) = 0 \)을 의미하고 이는 즉 \( (X^T X \theta ) = X^T Y \)를 의미한다.
또한, 여기서 간단하게 언급할 것은 위에서 구한 theta hat의 식을 한 번 보자. \( X^T X ) ^{-1} X^T Y \) 에서 \( X^T X ) ^{-1} X^T \)를 보면 이는 Moore-Penrose Psuedoinverse를 의미한다.
위 식을 보면 \( X^T X )^{-1} \)의 식이 있는데 이는 매우 계산하기가 힘들다. 따라서 Moore-Penrose Psuedoinverse 를 통해서 ( X^T X ) ^{-1} X^T = X^{-1}\)로 계산을 하여 구한다.

다음 포스팅에선 이렇게 구한 \( \theta \)를 iterative 한 방법 Gradient Descent 방법으로 구하는 것을 보겠다.