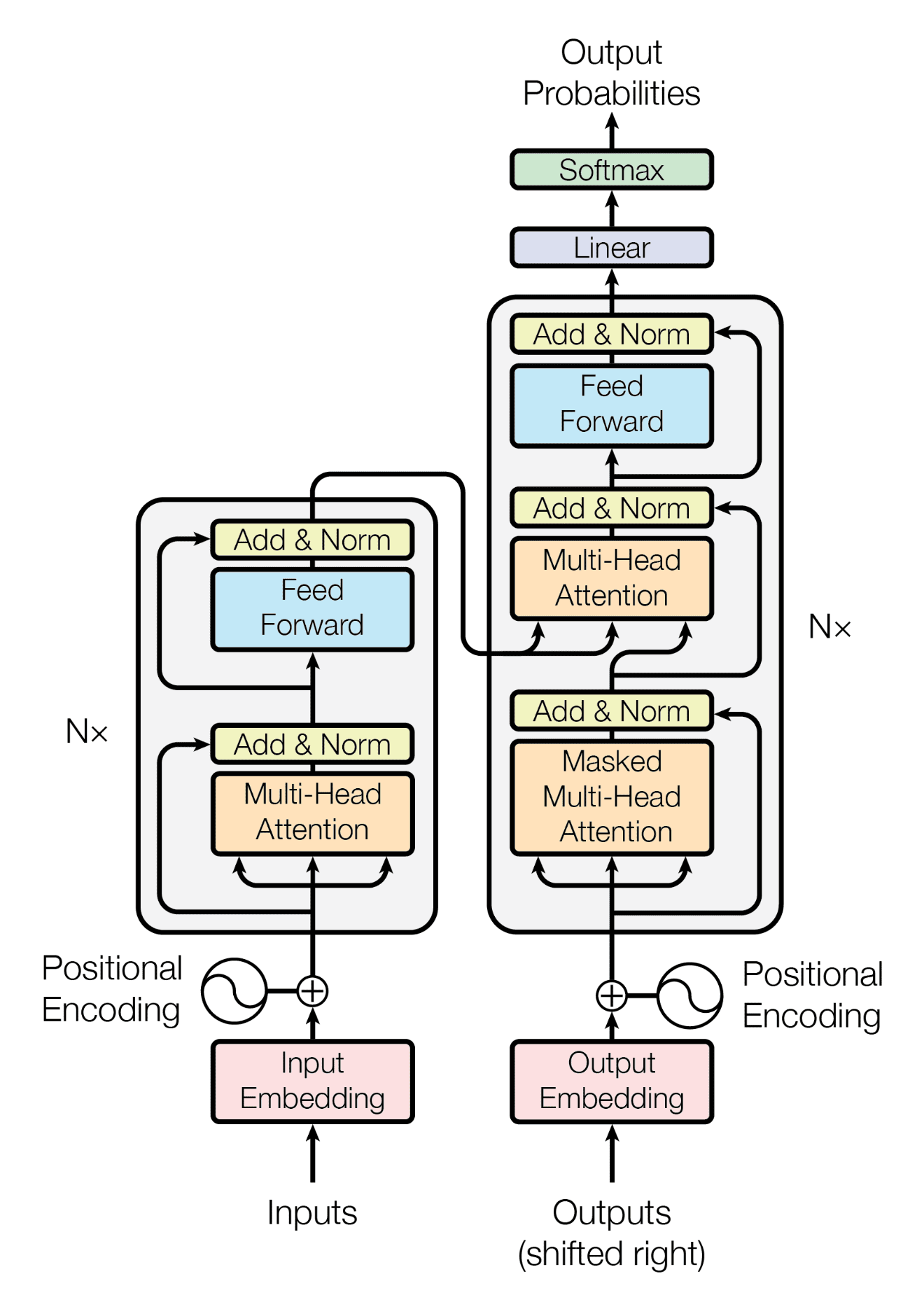
Attention is all you need
https://www.youtube.com/watch?v=AA621UofTUA&t=192s
나동빈님 강의를 기반으로 설명을 진행한다.
Seq2Seq 는 하나의 context vector가 source sentence(input)의 모든 정보를 가지고 있어야하므로 bottleneck이 발생한다. 따라서 이로 인해 성능 저하가 일어난다. 따라서 이를 해결하기 위해 source sentence에서의 output 값 전부를 input으로 받는다. 따라서 고정된 크기의 context vector로 압축하는 것이 아니라 이를 입력값으로 다시 처리해주면서 출력단어를 만들면 더욱 성능이 좋아진다는 것이다.
Seq2Seq 포스팅
2021.11.01 - [논문 정리] - Sequence to Sequence Learning with Neural Networks(Seq2Seq)
이런 아이디어를 기반으로 나온 것이 Seq2Seq with Attention이다.
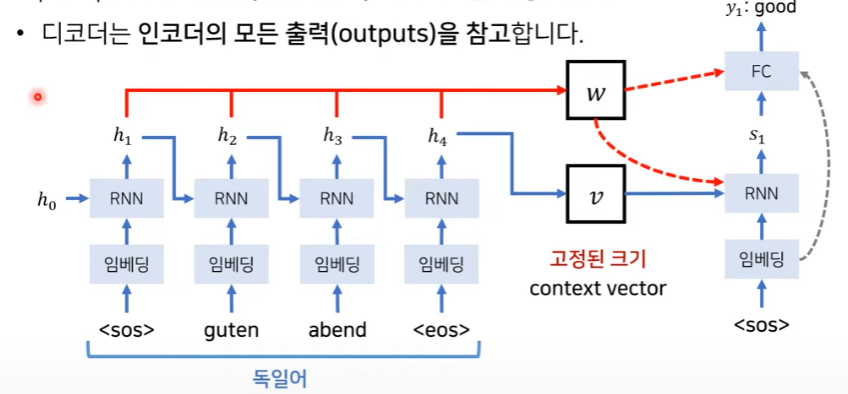
Attention mechanism을 통해 encode의 모든 output들을 attention score로 만든다. 위 그림에서도 알 수 있듯이 각각 source sentence의 출력값 \( h_{i} \)들을 attention weight w에 다 저장하는 것을 볼 수 있다. 즉, 이를 통해서 context vector 하나만 고려하는 것이 아니라 weight 값들을 모두 decoder의 입력으로 넣어줘서 모든 source sentence를 더 효율적으로 고려할 수 있게 한다.
이렇게 encoder에서 나온 attention weight 와 context vector는 decoder에서 다음과 같이 처리된다.
i = 현재의 decoder가 처리 중인 index라고 하고, j는 각각의 encoder 출력 index라고 할 때
$$ e_{ij} a(s_{i-1},h_{j}) $$
$$ a_{ij} = \frac{exp(e_{ij})}{\sum_{k=1}^{T_{x}}exp(e_{ik})} $$
로 energy와 weight 가 각각 도출된다. energy에서 \( s_{i-1} \)은 decoder가 이전 출력의 hidden state이고, \(h_{j}\)는 encoder 파트의 각각의 hidden state이다. 이를 정리하면 decoder에서 이전의 출력했던 값은 \( s_{i-1}\)이고, 이 정보와 encoder의 모든 출력값과 비교해서 energy 값을 구하는 것이다. 이는 encoder의 전체 출력값 중 어떠한 값이 이전의 출력했던 값과 가장 유사한지를 알 수 있는 것이다. 그리고 weight 값은 이러한 energy 값에 softmax를 취한 값으로 비율적으로 각각의 h이 decoder의 이전값과 유사한지 나타낸 것이다. 이래서 이는 attention score라고도 한다.
따라서 이렇게 나온 attention score와 hidden state값을 곱해주면서 context vector의 역할을 할 수 있게 된다. 이는 식으로 다음과 같이 나타난다.
$$ c_{i} = \sum_{j=1}^{T_x} a_{ij}h_j $$
이러한 attention weight를 이용하여 각 출력이 어떤 입력 정보를 참고했는지 시각화 할 수 있다.

따라서 Transformer로 알려진 Attention all you need 논문은 이러한 Attention 기법만 잘 활용해도 RNN과 CNN을 전혀 활용하지 않고도 잘 처리할 수 있다라는 논문이다.
그러나 RNN이나 CNN을 사용하지 않으면 문장 내의 순서를 알기 힘들다. 따라서 이를 극복하기 위해 본 논문에서는 Postional Encoding 개념을 적용하여 이러한 문제를 해결한다.
Transformer
Transformer 이전의 embedding은 단어의 개수 x embedding dimension (가로 x 세로) 로 이루어진다. (embedding dimension = hyper-parameter)
반면에 Transformer는 RNN을 사용하지 않기 때문에 embedding 과정에서 Postional Encoding이라는 특별한 과정을 거친다. 일반적인 embedding matrix에 postional encoding을 element wise로 더해서 단어의 위치(순서) 정보를 표현한다.
이러한 입력 문장에 대한 정보 + 위치에 대한 정보가 포함된 값을 Multi-Head Attention에 넣어준다. 여기서 Encoder 파트에서의 Attention은 self-attention이라고 부르고 각각의 단어가 서로에게 어떠한 연관을 갖고 있는지에 대한 정보를 추출하는 파트이다.
또한, 여기서 추가적으로 residual learning을 사용한다. 즉, Multi-head attention을 거친 값과 postional encoding+ input embedding matrix의 값을 서로 더해준다. 그 이후 noramlization을 해준다. 이는 다음의 그림과 같이 표현된다.
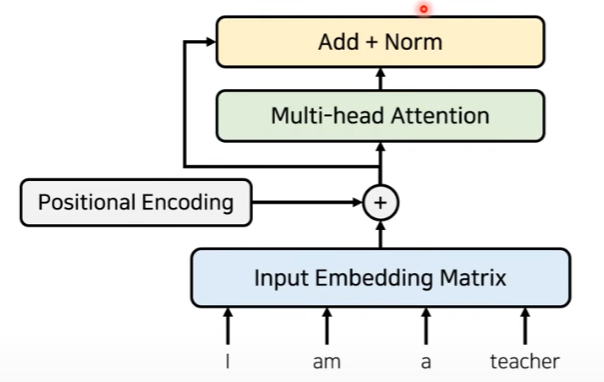
위 그림에서 추가적으로 feedforward layer를 해주고 이를 또 residual connection을 해주면서 transformer의 하나의 layer가 완성된다.

이러한 layer들을 여러개 쌓아서 encoder가 구성이 되고 각각의 layer들은 파라미터가 다 다르다. 이러한 layer들을 쌓는 것이기 때문에 입력되는 dimension과 output dimension은 서로 같다. 이 layer 구조는 decoder에서도 동일하게 적용되며 다음의 그림과 같다.
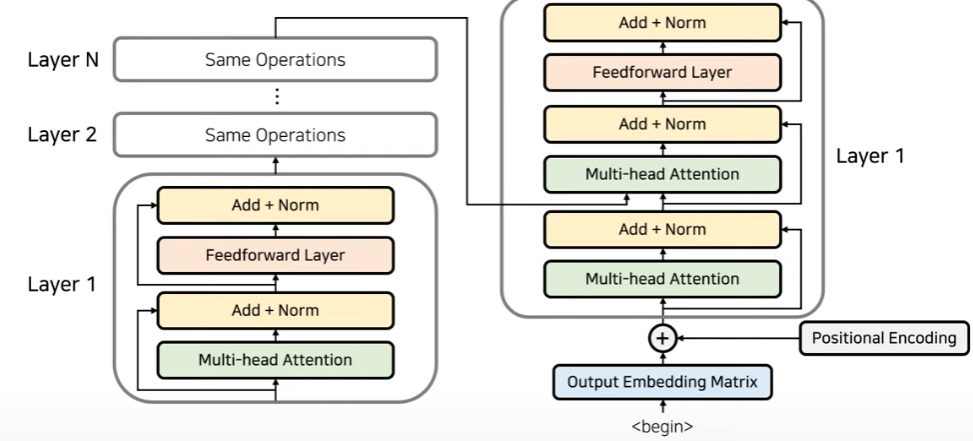
decoder에선 가장 마지막에 encoder에서 출력된 값을 넣어줌으로써, 출력할 때 마다 어떤 단어에게 가장 초점을 맞춰야되는지 알려주기 위함이다.
decoder는 encoder layer와 다르게 attention을 두번 해주는데 첫번째 attention은 output sentence에 대해 서로가 서로에게 각각의 가중치를 가지는 지 구하기 위함이고, 두번째 attention은 encoder한 정보에 대한 attention을 함으로써 각각의 출력되고 있는 단어가 source sentence의 어떤 단어와 연관성이 있는지를 파악하는 것이다.
Transformer는 이렇게 Encoder - Decoder를 거치면서 번역이 수행이 되고 하나의 encoder와 decoder로 수행이 된다. 즉, 입력 문장 자체의 길이가 한 번에 들어감으로써, 하나의 encoder만 필요한 것이다. 이는 입력 단어의 개수 만큼 encoder decoder cell이 생성되는 것과 다른 것을 볼 수 있다.
## Multi-head Attention

Attention을 이해하기 위해선 Query, Key, Value가 무엇인지 알아야한다. Attention은 어떠한 단어가 어떠한 단어와 연관성이 있는지 계산하는 것이다.
여기서 Query는 무엇인가를 물어보는 주체이고, 물어보는 대상이 Key 이다.
예를 들어, I am a teacher 라는 문장이 있을 때 I라는 단어가 I am a teacher 라는 문장과 얼마만큼 연관성이 있는지 계산할 때, I 라는 단어는 Query가 되고 I am a teacher의 각각 단어들은 Key 가 되는 것이다. 이렇게 얼마만큼 연관이 있는지 score를 구하고, 이러한 score들과 value 값을 곱해주어서 결과적인 attention value를 구할 수 있다.
위 그림을 통해서 설명하면, Queary 값과 attention을 수행할 단어들 Key 와 각각 행렬곱(Matmul)을 수행한다. 그 후 scaling을 해주고 필요하다면 mask 처리까지 해준 다음에 softmax를 처리 하면서 어떤 단어와 가장 연관이 있는지 확률적인 점수를 나타낸다. 마지막으로 value 값과 행렬곱을 수행해주면서 최종적인 attention score가 나오게 된다.
Multi-head Attention에서는 scaled dot-product attention 을 수행하는데 입력값이 들어왔을 때 한번만 수행하는 것이 아닌 h개로 나누어 하나의 sentence에 대해 h개의 value, key , query로 나누어 수행한다. 이렇게 하는 이유는 서로 다른 attention concept을 만들어서 더욱 다양한 특징들을 학습할 수 있도록 유도해주는 것이다. head의 개수인 h개로 각각 scaled dot-product attention을 수행해주고 이를 concat한 다음에 linear layer를 거쳐 output 값을 내보낸다. 이렇게 입력값과 출력값의 dimension을 같게 만들어서 attention layer를 쌓을 수 있게 해준다.
이러한 multi-head attention layer를 수식으로 표현하면 다음과 같다.
$$ Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$$
$$ head_{i} = Attention(QW_{i}^{Q},KW_{i}^{K},VW_{i}^{V} )$$
$$ MultiHead(Q,K,V) = Concat(head_{1},\cdots,head_{h})W^{O} $$
첫번째 식을 설명하면 Attention 을 할 때 Query(Q), Key(K), Value(V) 3개 인자를 받는다. 여기서 Query와 Key 값을 dot prdocut 한다. 그리고 각각의 key dimension에 root 값을 씌운 것으로 나누고 이를 softmax 취한다. 여기서 scaling factor \( \sqrt{d_k} \)를 취해준 이유는 gradient vanishing 문제를 피하기 위함이다. (softmax의 특성을 고려해서) 그리고 이러한 score 값과 value 값을 곱해서 attention value 값을 나타낼 수 있다.
그리고 두번째 식은 입력으로 들어온 각각의 값에 대해서 서로 다른 linear layer를 거치도록 만들어서 h개의 서로 다른 Q,K,V 가 나오게 하는 것이다.
그리고 마지막 식은 이렇게 나온 head들을 모두 concat 하여 output matrix와 곱해주면서 최종적인 output 값이 산출된다.
### Key, Query, Value

Query, Key, Value는 단어의 embedding matrix를 통해 생성된다. 이는 embedding dimension 를 head의 개수 h로 나눈 각 Q,K,V의 dimension이 구성된다.
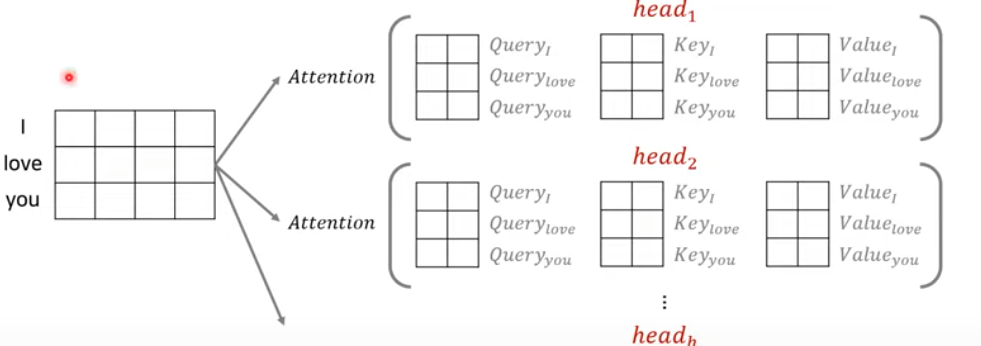
예를 들어 위의 그림처럼 love라는 단어의 embedding 차원이 4이고, head의 개수가 2라고 가정한다. 그러면 Q,K,V의 Weight의 차원은 4x2로 matrix가 구성이 된다. 이에 따라서 행렬곱 연산을 통해 1x 2의 Query, Key, Value의 matrix가 구성된다.
이렇게 구성된 Query, Key, Value 값은 행렬 곱과 scaling으로 연산이 되고 I love you 라는 단어로 예를 들자면 다음과 같다.
Query I 라는 단어에 Key I, Key love, Key you와 행렬곱으로 연산이 된다. 그리고 이를 scaling factor로 나누어주고 softmax를 취해 각 Key 에 대한 점수를 반환한다. 그리고 이를 Value I, Value love, Value you와 곱해주고 더해주어서 attention matrix를 반환한다.
\( QK^{T} \)의 행렬과 mask matrix를 사용하여 특정 단어는 무시하고 학습을 할 수도 있다. \( QK^{T} \)와 mask matrix 를 element wise로 곱해주어서 해당 단어를 무시하게 할 수도 있다.

단어를 무시하기 위해 mask matrix 위치에 무한한 음수값을 넣어서 softmax가 0을 반환할 수 있도록 한다.
이러한 과정을 거치고 각각의 head 마다 Q,K,V에 대한 matrix가 나오게 된다.
각각의 head마다 나온 Q,K,V의 값을 concat을 한다. 이렇게 되면 결국 output 의 dimension은 초기의 input embedding dimension과 같아지게 되는 효과를 얻을 수 있다.
## Positional Encoding
Positional Encoding은 주기 함수를 활용한 공식으로 각 단어의 상대적인 위치 정보를 네트워크에게 입력하는 것이다. 수식적으로 보면 다음과 같다.
$$ PE_{(pos,2i)} = sin(pos/10000^{2i/d_{model}}) $$
$$ PE_{(pos,2i+1)} = cos(pos/10000^{2i/d_{model}}) $$
여기서 pos는 각각의 단어 번호 (word to index 할 때 그 index 값) 가 되고, i는 각각 단어의 embedding 값의 위치를 의미한다. \( d_{model} \)은 embedding의 차원을 의미한다. 꼭 sin과 cos뿐만 아니라 주기가 있는 상대적인 위치를 나타내는 함수라면 어떤 함수든 상관이 없다.

따라서 이렇게 구성한 postional encoding 값과 일반 embedding 값을 element-wise로 더해주어서 단어의 위치 정보를 알 수 있게 한다.
## Transformer Full Architecture