Probability Distribution
간단한 요약 버전은
2022.07.17 - [Probability & Statistics] - 확률분포 정리
확률분포 정리
## Uniform Distribution 특정 구간 내의 값들이 나타날 가능성이 모두 균등한 확률 분포를 의미 \( E(X) \) \(\frac{1}{2}(a+b) \) \( Var(X) \) \( \frac{1}{12}(b-a)^{2} \) ## Bernoulli distribution 확률..
bigdata-analyst.tistory.com
Probability Distribution은 왜 공부할까?
이는 바로 Density Estimation을 위한 것이다.
그러면 Density Estimation이란 무엇인가? Density Estimation이란 제한된 관찰값이 주어졌을 때, 이러한 관찰값을 설명할 수 있는 확률 모델을 구하는 것이다.
이러한 Density Estimation에는 두가지 접근 방법이 있는데 Parametric apporach와 Nonparamteric approach 로 나뉘어진다.
Parametric approach는 분포의 특정한 함수를 구하는 방법이다. 이러한 방법의 예시로는 binary variables, Multinomial variables, Gaussian distribution 등이 있다.
Nonparameter approach는 parameteric approach와 정반대가 되는 개념으로 확률의 형태가 data의 크기에 의존적으로 모델링 되는 것이다. 이러한 방법의 예시로는 Kernel density estimator, NN-method 등이 있다.
즉, parameteric approach는 특정한 확률에 대한 분포를 구하는 것, nonparameteric approach는 확률에 대한 것이 아닌 데이터의 크기에 따른 분포를 정하는 것 이다.
본 포스팅에서는 paramteric approach를 중점적으로 파악할 것이다.
이러한 paramter를 찾는 방법과 연관된 두가지 관점은 전 포스팅에서도 설명한 Frequentist와 Baysian 방법이다.
Frequentist는 MLE(Maximum Likelihood Estimation)을 통해 parameter를 찾고, Bayesian 관점에서는 MAP(Maximum a Posteriori)로 파라미터를 찾는다.
## Paramteric Distributions
Paramteric Distribution은 parameter approach 방법으로 \( p(x| \theta )\)에서 paratmer \( \theta\)를 찾는 것을 목적으로 한다.
여기서 \( p(x| \theta )\)가 주어진 dataset에서 데이터 \( \mathrm{x} = \{ x_{1}, \cdots , x_{N}\)을 잘 설명하기 위한 \( \theta \)를 찾는 것이다. 따라서 최적의 \( \theta^{*} \)를 찾고 이에 대한 분포를 찾는 것이 paramteric approach의 목적이다.
이제 특정한 확률분포 \( p(x| \theta) \) 에 대한 확률 분포의 종류를 알아보자.
## Binary Variable
Binary Variable은 간단한 동전 던지기 예시로 표현이 된다.
동전의 앞면이 나왔을 때에는 1로, 뒷면이 나왔을 땐 0이라고 하자. 다음과 같은 식으로 확률을 부여할 수 있다.
앞면이 나왔을 때 확률을 \( p(x=1 | \mu ) = \mu \) 라고 하고, 이 \( \mu \) 자체가 parameter 가 된다.
이러한 시행을 Bernoulli 시행 이라고 하고, 이러한 시행을 해서 얻은 분포를 Bernoulli distribution 이라고 한다.
Bernoulli Distribution은 다음과 같은 성질을 따른다.
$$ Bern(x| \mu ) = \mu^{x} ( 1- \mu )^{1-x} $$
$$ \mathbb{E}(x) = \mu $$
$$ Var(x) = \mu (1-\mu) $$
이러한 Bernoulli 시행은 동전 하나에 대한 분포이다.
그러면 만약에 동전이 하나가 아닌 여러개인 N개 일 때는 어떻게 나타낼까
이는 Binomial Distribution이라고 한다.
Binomial distribution은 Bernoulli distribution을 N 차원으로 확장하는 것이라고 생각하면 된다. 그리고 이는 다음과 같은 특징을 갖는다. 먼저 식에 대한 notation을 보면 동전으로 예를 들면,
앞면이 나온 횟수를 m 이라고 하고, N은 시행 횟수, \( \mu \)는 각 시도에서 앞면이 나올 확률을 말한다.
$$ Bin(m | N, \mu ) = {N \choose m} \mu^{m} (1-\mu)^{N-m}$$
$$ \mathbb{E}(m) = \Sigma_{m=0}^{M} m Bin (m | N , \mu ) = N \mu $$
$$ var(m) = \Sigma_{m=0}^{N} (m - \mathbb{E}m)^{2} Bin (m | N , \mu) = N \mu (1- \mu ) $$
이러한 Binomial Distribution을 보면 Bernoulii distribution의 특징에서 시행횟수 N을 곱해준 것과 동일하다(expectation, variance)
이러한 Binomial distribution의 예시 graph를 보자면 Bin(m|10,0.25) 일 때, 10시행해서 m이 나올 확률이 0.25 라는 뜻을 가진 시행에 대한 분포는

이러한 Binomial Distribution을 ML 관점에서 보았을 때 paramter를 도출하는 과정은 다음과 같다.
Bernoulli distribution을 중심으로 살펴보고, 이 distribution에서 도출하고자 하는 parameter는 \( \mu \) 이다. 이를 Frequentist 관점으로 MLE로 풀어보자.
Data \( D = \{ x_1 , \cdots , x_n \} \)이 주어진다. 이 때, x는 0 or 1 이 된다. 하나의 사건 확률을 m 이라고 하고 그에 반대되는 확률을 N-m 이 주어진다고 하자.
이러한 주어진 값들을 통해 \( p(D | \mu ) \)를 최대화 시킨다. (Maximum Likelihood)
이를 풀면 다음의 과정과 같다.
$$ p(D | \mu) = \Pi_{n=1}^{N} p (x_n| \mu) = \Pi_{n=1}^{N} \mu^{x_n} ( 1- \mu )^{1-x_n} $$
먼저 위처럼 data의 joint 확률을 구한다. 그리고 위 식에 log 를 취해준다.

log 를 취해주면 곱셈이 덧셈으로 바뀌므로 sigma가 되고, 지수는 밑으로 떨어진다.
그러면 이 식에서 이상적인 \( \mu \) 값은 결국 \( \frac{\delta \ln p(D| \mu )}{\delta \mu} = 0\) 이 될 때이다. 따라서 이를 미분해서 계산을 하면 \( mu_{ML} = \frac{1}{N}\Sigma_{n=1}^{N} x_n = \frac{m}{N} \) 이 된다.
이는 즉, \( \mu \) 자체는 어떠한 경우의 수 (예를 들어 동전 앞면이 나올 확률) 이기 때문에 \( \frac{m}{N} \)은 이러한 \( \mu \)의 의미를 잘 반영했다고 볼 수 있다.
하지만 이러한 관점 즉, frequentist의 단점은 경우의 수가 적을 때 이다.
만약 경우의 수 즉 N이 3이고 이러한 데이터들은 모두 1 이라고 가정하자. 즉, 동전을 던졌을 때 3번 모두 앞면이 나온다는 것이다. 그러면 Frequentist 관점으로 해석하였을 때는 다음에 던져도 무조건 동전은 앞면만 나온다는 예측을 하게 된다.
하지만 이는 실제 상황에서 맞지 않기 때문에 데이터 수가 적을 때 Frequentist 관점은 문제가 된다.
## Beta Distribution
Beta distribution은 확률에 대한 확률 분포이다. 이는 앞서 말한 \( \mu \) 가 [0,1] 사이로 범위가 제한되어 있다는 것이다.
beta distribution은 다음과 같은 식이 도출된다.

beta distribution은 a와 b에 따라서 다양한 분포가 형성된다.
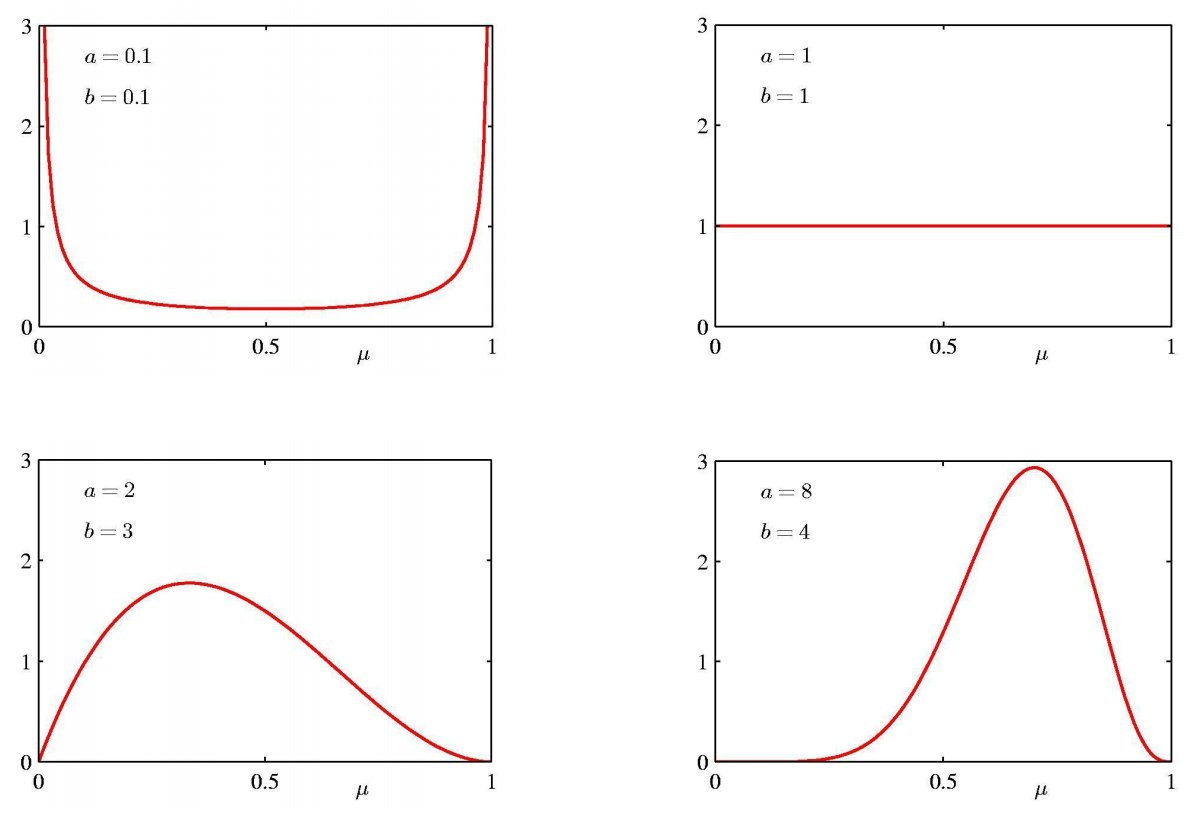
이러한 beta distribution은 Bayes' rule 관점으로도 표현될 수 있다.

맨 처음 식은 bayes' rule에서 다뤘던 Posterior는 Prior 와 Likelihood의 곱과 비례하다라는 식과 거의 동일하게 이뤄진다.
따라서 Posterior 와 Prior를 Beta distribution으로 하고 Likelihood를 Bernoulli distribution으로 설정한다. (따라서 beta distribution은 bayes' rule의 Prior distribution 으로 쓰인다는 말이 나옴)
이러한 식을 정리하면 Posterior distribution도 beta distribution으로 정의된다는 것을 증명할 수 있다.
위 식을 통해 알 수 있는 것은 Likelihood가 Bernoulli distribution 일 때, Prior와 Posterior는 Beta distribution으로 정의할 수 있다는 것이다. 이 말은 즉, Beta distribution은 Bernoulli distribution의 conjugate prior라는 뜻이다.
※ Conjugate Prior 은 Prior 분포와 Posterior 분포가 동일한 분포에 속하면 여기서의 사전 분포를 Conjugate Prior Distribution이라고 한다. 이럴 경우 Posterior distribution을 likelihood를 통해서 쉽게 추정할 수 있다. Conjugate Prior로 활용할 수 있는 분포는 대표적으로 normal distribution과 Binomial distribution 등이 있습니다.
이러한 식을 통해 Prior 와 likelihood = posterior 라는 것을 알아봤다. 즉 이 말은 Bayesian inference를 할 수 있다는 말이다. Bayesian inference는 frequentist와 다르게 Posterior를 최대화 하는 것이다. (MAP)
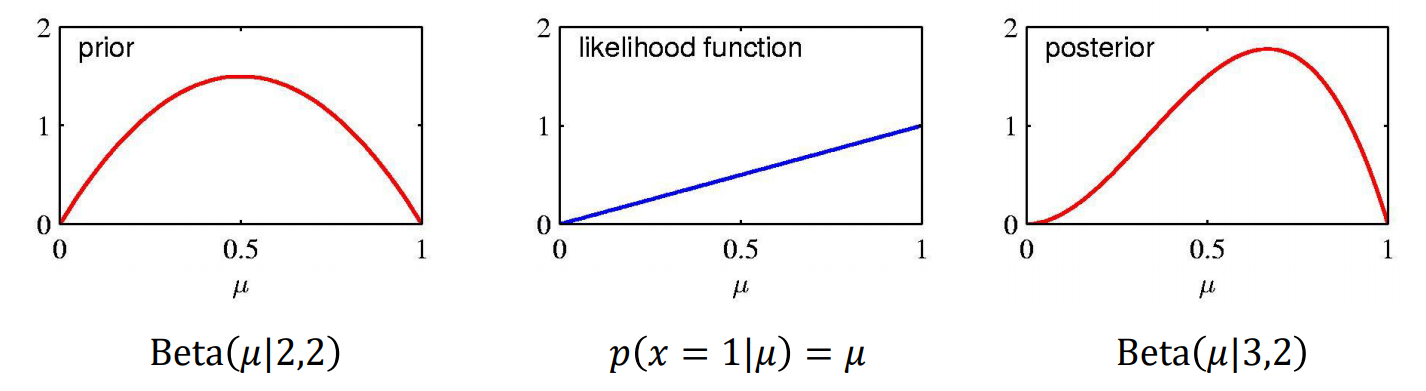
첫번째 distribution은 beta distribution을 가지는 prior distribution 이고, 두번째 distribution은 likelihood function이다.
따라서 이렇게 prior가 beta distribution을 따르고 likelihood가 bernoulli distribution을 따를 때, 앞선 식을 통해 beta distribution을 가지는 posterior distriubtion을 얻을 수 있다.
이러한 posterior distribution의 또 다른 성질에 대해 알아보자. Beta distribution을 따르는 posterior distribution의 dataset size( N )가 매우 커지게 되면
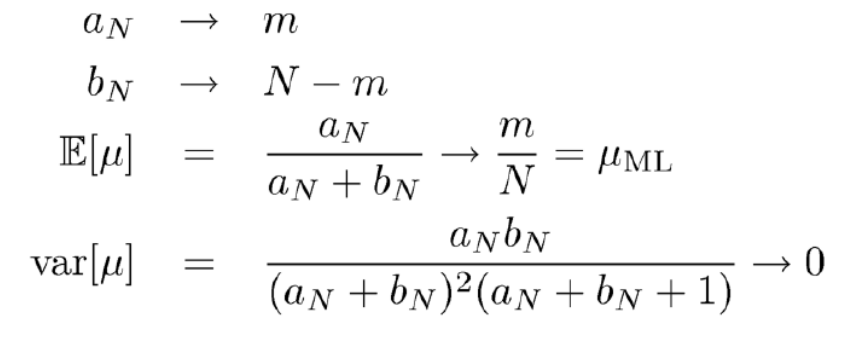
다음과 같이 수렴하게 된다.
여기서 주목할 점은 Expectation이다. 시도 횟수가 매우 커지게 되면 Expectation은 bernoulli distribution에서 본 Maximum likelihood를 통해 얻은 값과 동일해진다. 즉, \( \mu_{ML} = \mu_{MAP} \)가 된다. 이는 즉, MLE 방식으로 \( \mu \)를 구했을 때, 시도횟수가 적으면 문제가 생겼던 것을 시도 횟수가 적을 땐, \( \frac{a_N}{a_{N} + b_{N}}\)으로 되게 하고, 시도 횟수가 많아지면 MLE 방식으로 구한 것 처럼 \( \mu \)가 도출이 되어서 MLE의 단점을 극복한 것이라고도 해석할 수 있다. 이러한 해석을 증명하기 위해 MLE 방식이 아닌 MAP 방식으로 N이 한정되어있을 때, 다음에 어떠한 사건이 일어날 확률을 계산하면
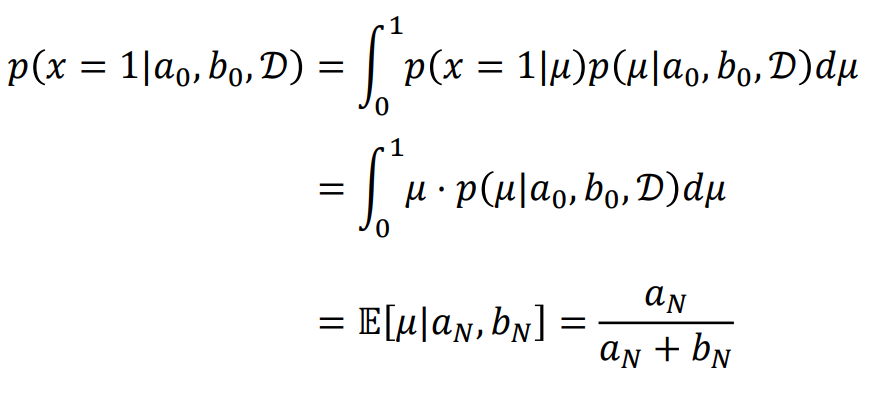
다음과 같은 식이 도출된다. MLE의 단점을 극복한 것을 수학적으로 증명할 수 있다.
지금까지 살펴본 Binomial distribution은 2개의 가능한 변수 중 하나를 선택하는 문제였다. 하지만 이를 확장시켜서 K개의 가능성 중 하나를 선택하는 문제를 다룬다. 즉, 그 전까진 앞뒷면을 가진 동전이었다면 이번엔 주사위로 확장하는 것이다.
그래서 그 전까지 통용하였던 확률 \( \mu \)를 각 시도에 대한 확률 \( \mu_k \)로 표현한다.
이렇게 Binomial 을 여러 개의 state로 확장한 것이 multinomial variable이다.
따라서 이는 간단하게 설명이 되고 이러한 distribution에 대한 성질도 간단하다.
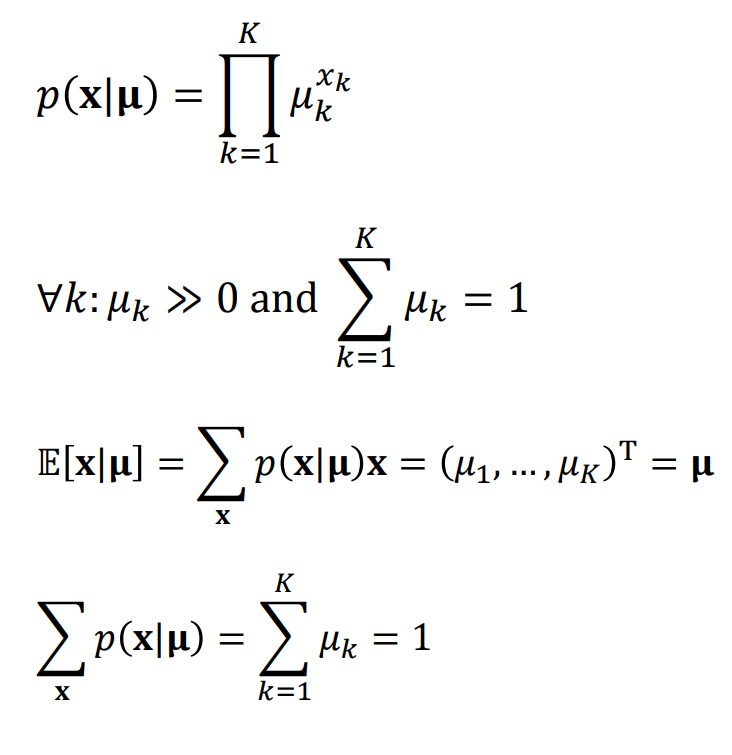
첫번째 식은 각 x에 대한 확률을 표현한 것이고 두번째는 각 state의 확률인 \( \mu_k \)는 0보다 커야하고 state의 모든 확률의 값은 1이 되어야한다는 것이다. 그리고 다음은 평균은 \( \mu \)가 되어야한다는 것과 각 확률에 대한 summation 값은 1이 되어야한다는 것이다.
그럼 이러한 multinomial distribution을 maximum llikelihood를 통해 \( \mu \)를 구하는 것이다.
먼저 likelihood를 구하면 \( p(D| \mu ) = \Pi_{k=1}^{K} \mu_{K}^{m_k} \) 가 된다.
이렇게 likelihood를 구하고 그 전처럼 \( p(D| \mu ) \)를 \( \mu \)에 대해서 미분을 바로 하는 것이 아니라 \( \mu \)에 대한 constraint를 걸어줘야한다. 이렇게 제약조건을 주면서 라그랑지 승수법을 사용하여 \( \mu \)를 구한다.
constraint는 \( \Sigma_{k} \mu_k = 1 \) 이고 이에 따른 라그랑지 승수( \( \lambda \) ) 법을 이용한 최적화 식은 다음과 같다.
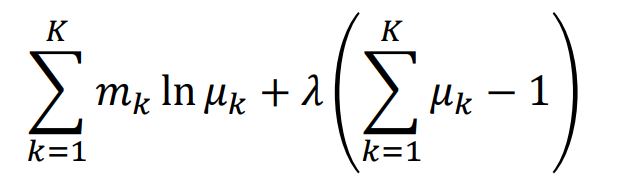
이에 따라서 \( \mu_k \)와 \( \mu_{ML} \)을 구하면
$$ \mu_k = -m_{k}/ \lambda $$
$$ \mu_{k}^{ML} = m_{k}/N $$
이 도출된다.\propto
지금까지 알아본 multinomial variable은 multinoulli distribution이라고 말할 수 있다. (시행횟수가 1번 이므로)
이제 알아볼 것은 시행 횟수가 N 번인 multinomial distribution에 대해 알아보자
이러한 Multinomial distribution은 multinoulli를 N번으로 확장한 것이고 다음과 같이 이뤄진다.
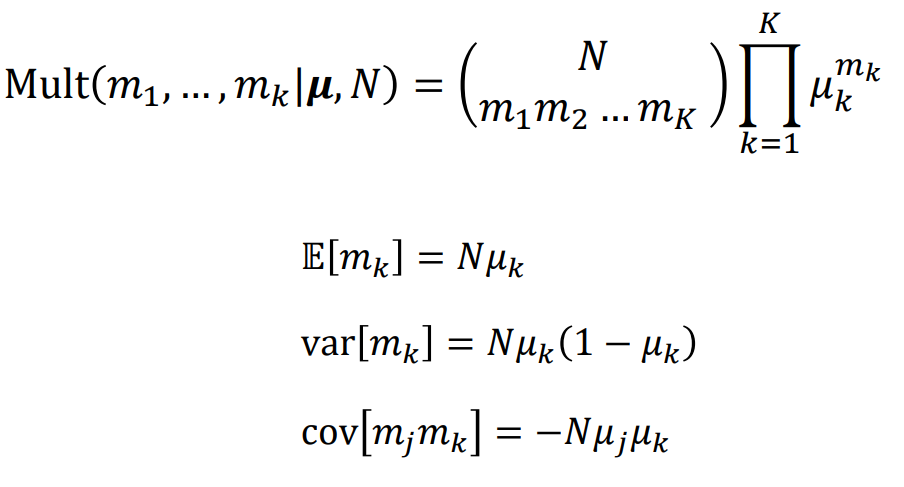
여기서 \( m_k \) 는 k 번째 state가 몇번 나오는지에 대한 값이다. 즉, k=6 인 주사위라고 했을 때, 주사위를 던져서 특정한 숫자가 몇번 나오는지에 대한 횟수라고 생각하면 된다.
따라서 Multinomial distribution은 이러한 식을 가지고 있으며 이에 대한 자세한 식 유도는 생략한다.
## Dirichlet distribution
Dirichlet distribution을 알아보기 전에 Posterior에 대해 다시 한 번 생각해보자
$$ P( \mu | D) \propto P(D|\mu) P(\mu) $$
posterior는 likelihood와 prior의 곱과 비례한다는 것이다.
beta distribution에서 설명했듯이 likelihood가 Bernoulli distribution을 따르면 prior distribution은 beta distribution을 따르고 이는 posterior distribution도 Beta distribution을 따른다.
그러면 만약에 likelihood가 multinomial distribution을 따르면 prior와 posterior의 distribution을 어떤 것을 따를까?
바로 Dirichlet distribution이다.
Dirichlet distribution은 다음과 같은 식을 따른다.
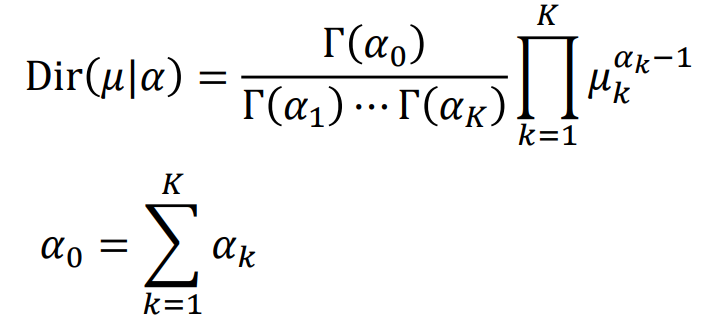
이러한 식을 갖고 있다는 것만 알고 넘어간다.
마지막으로 conjugate prior의 개념을 넣어 정의하자면 Dirichelt distribution은 Multinomial distribution의 conjugate prior이다.
## Gaussian Distribution
언제 어디에서나 쓰이는 Gaussian distribution에 대해 알아보겠다.
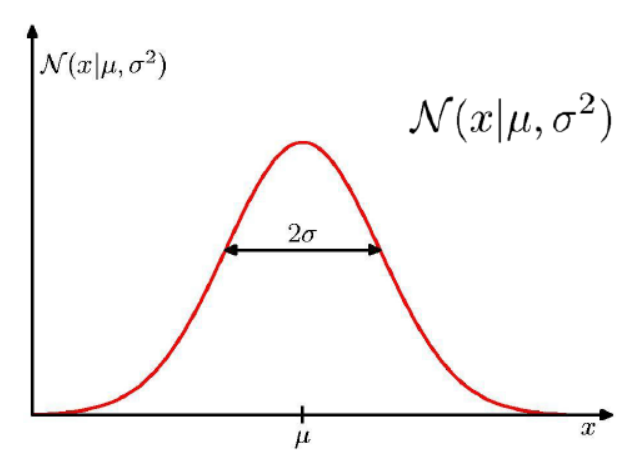
Gaussian distribution은 중심이 \( \mu \) 이고 variance가 \( \sigma^{2} \)인 distribution이다.
이러한 guassian distribution의 식은
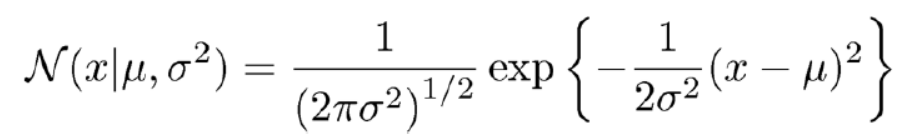
이런 식으로 된다.
사실 이는 너무 잘 알려진 것이므로 이에 대한 다른 설명은 하지 않겠다.
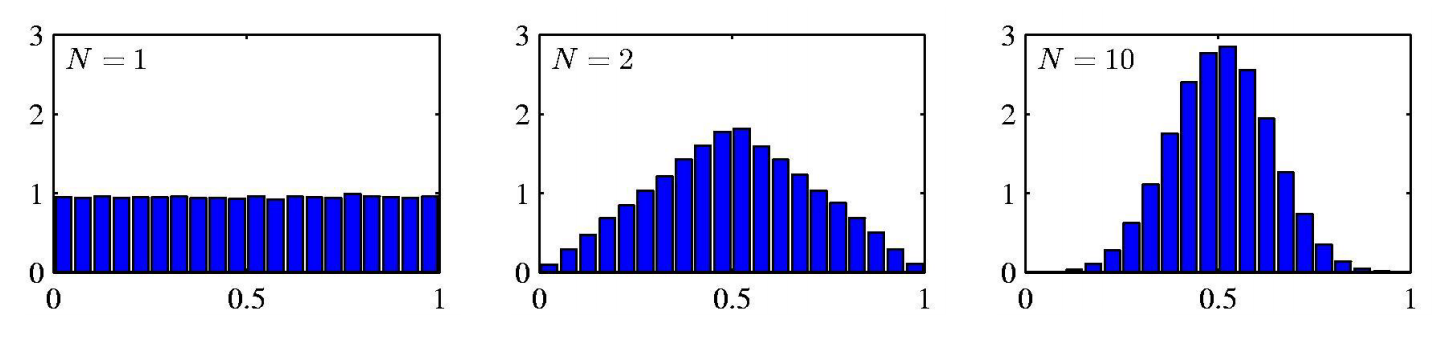
Gaussian distribution과 연관되어있는 것은 Central Limit Theorm으로 한국말로 중심극한정리이다.
Central Limit Therom은 Independent 하고 identity한 N개의 random variable의 distribution의 summation이 N 개의 개수가 커짐에 따라서 random variable distribution은 Gaussian distribution을 띈다는 것이다.
## Multivariate Gaussian
Multivariate Gaussian(Gaussian의 다변량)를 Geometry 관점에서 살펴보겠다.
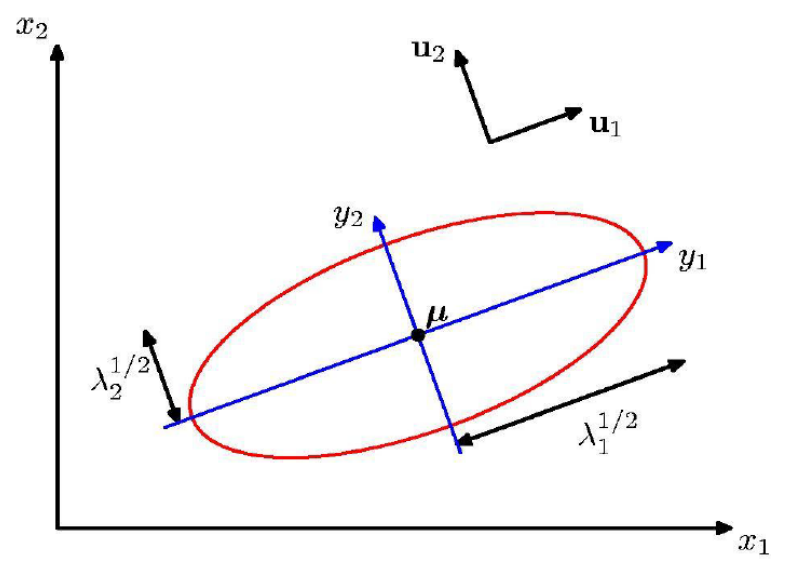
여기서 \( \mu \)는 타원에 대한 중심점이고, covariance는 타원의 지름과 연관이 되어있다는 것을 기억하면 된다.
이에 대한 moment는 기댓값 \( \mathbb{E}(x) \)와 covariance와 연관되어 있는 제곱의 기댓값 \( \mathbb{E}(xx^{T}) \)를 중심적으로 본다.
기댓값은 잘 알려진 것처럼 \( \mathbb{E}(x) = \mu \)가 나오게 된다.
그리고 \( \mathbb{E}(xx^{T}) = \mu \mu^{T} + \Sigma \) 가 된다. 그리고 이를 이용해서 covariance를 구하면
\( cov(x) = \mathbb{E}[(x - \mathbb{E}(x)) (x - \mathbb{E}(x))^{T} ] = \Sigma \)가 된다.
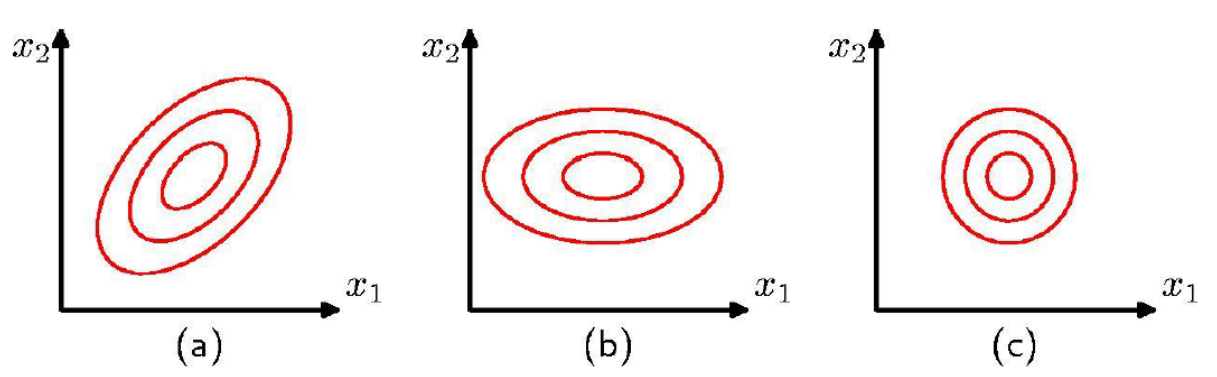
위의 그림은 covariance \( \Sigma \)와 관련이 있다. (a)는 일반적인 경우에 해당이 되고 (b) 같은 경우는 \( \Sigma \)가 diagonal matrix일 경우이다. diagonal matrix 같은 경우에는 대각원소 외에 모두 0이 되는데 이는 x1 과 x2가 서로 연관이 없다라는 것을 의미한다. (c)는 \( \Sigma \)가 Identity Matrix * scalar = \( \lambda I \)값일 때를 의미한다. 즉 이는 x1과 x2가 같은 variance를 가진다는 것을 의미한다.
다음으로 Gaussian distribution에 대해 MLE를 해보자이는 앞서 진행한 것 처럼 log-likelihood function \( \ln p(X| \mu, \Sigma \)를 구한 후 likelihood를 \( \mu \)로 미분한다.이에 대한 식은 다음과 같다.
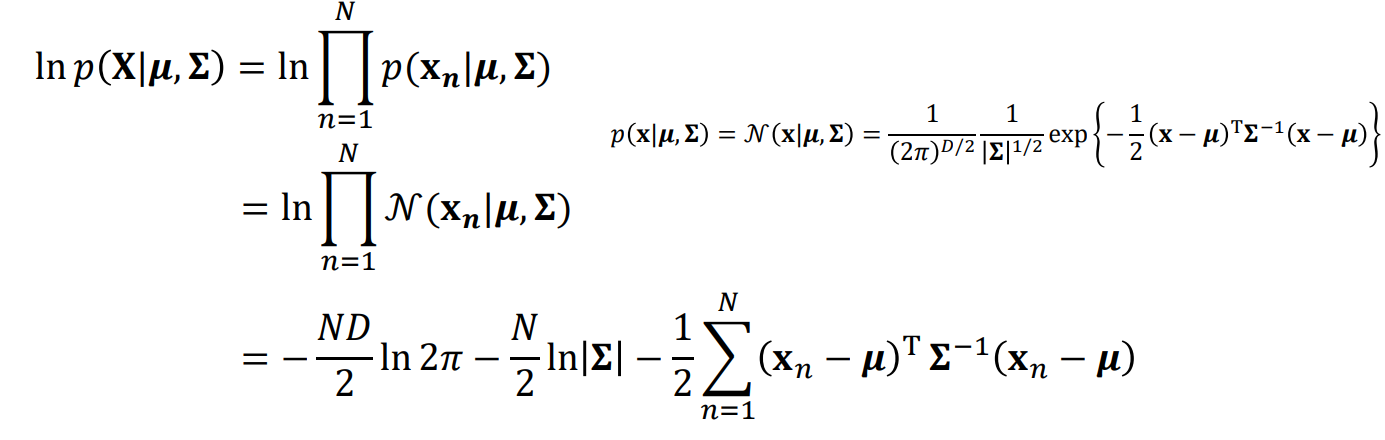
위 식은 Gaussian distribution의 likelihood이다. 그리고 이를 \( \mu \) 에 대해 미분하면
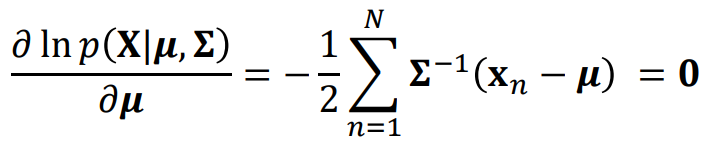
다음과 같은 식을 통해 극대값을 찾을 수 있다.
따라서 이 식을 풀면 \( \mu_{ML} = \frac{1}{N} \Sigma_{n=1}^{N} x_n \) 이 된다.
그러면 이를 \( \mu \)에 대해서만 미분을 하는 것이 아닌 \( \Sigma \)에 대해서도 미분을 해보자.
그러면 \( \Sigma_{ML} = \frac{1}{N} \Sigma_{n=1}^{N} (x_n - \mu_{ML})(x_n - \mu_{ML})^{T} \) 가 된다.
그러면 이를 MLE를 통한 것이 아닌 즉, Frequentist 관점이 아닌 Bayesian 관점에서 구해보자
먼저 Likelihood function을 구한다.
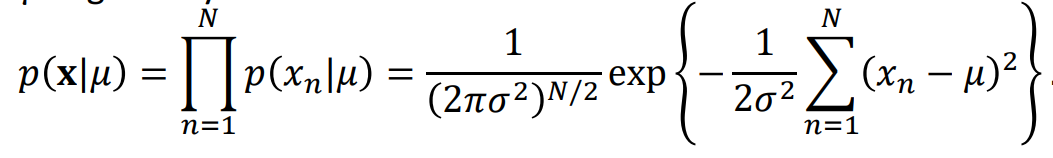
이 likelihood를 구할 때, \( \sigma^{2} \)는 알고 있다고 가정한다.
이 때, likelihood는 gaussian distribution을 따른다.
그러면 posterior와 likelihood x piror 가 비례하다라는 관계에서 likelihood가 guassian distribution을 따르고 \( \sigma^2 \)을 아는 상태에서는 prior의 distribution은 guassian distribution이 되고, 이는 posterior 도 gaussian distribution을 따른다.
즉, 이를 다시 말하면 gaussian distribution은 gaussian distribution의 conjugate priror 이다.
따라서 Prior distribution을 \( p (\mu ) = N (\mu | \mu_0 , \sigma^{2}_{0} \)으로 설정한다.
그리고 Posterior distribution을 풀어서 결과를 보면
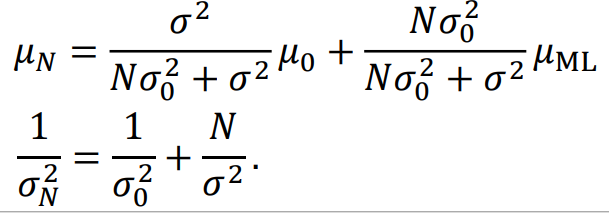
다음과 같이 나오게 된다.
따라서 이러한 값은 N의 크기에 따라 달라지게 되는데 이는 다음의 표처럼 정리된다.
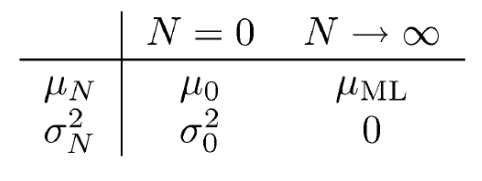
결국 N이 커질때는 \( \mu_{ML} \)과 가까워지게 된다.
이러한 결과를 그림으로 distribution을 나타내면 다음과 같다.
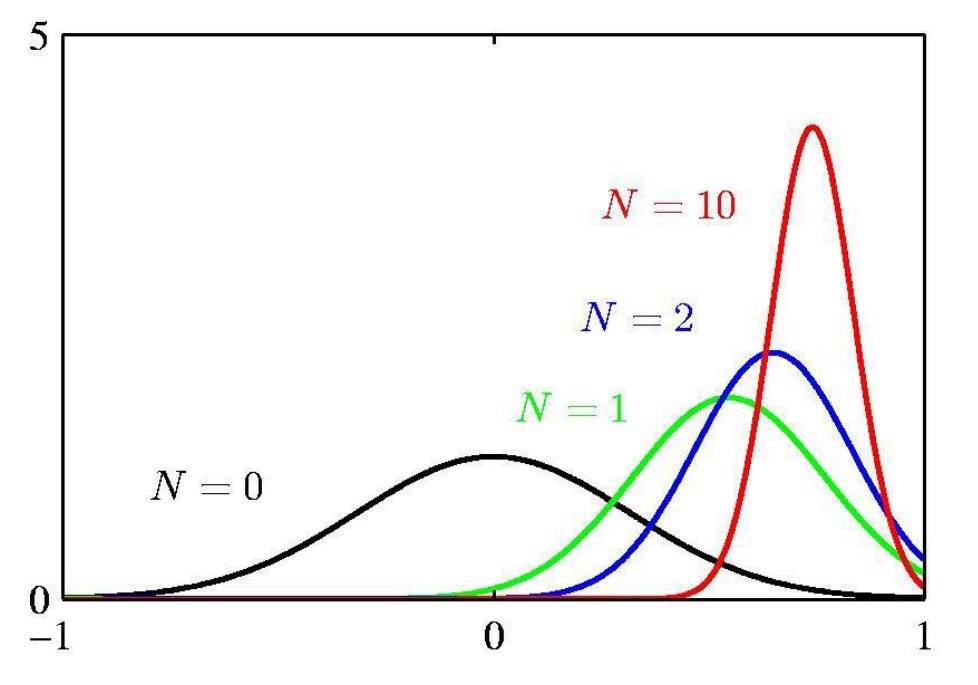
## Mixture Gaussian
Mixture Gaussian은 말 그대로 가우시안의 집합이다. Single Gaussian이랑 Mixture Gaussian 과의 차이를 잘 나타내주는 그림을 보자
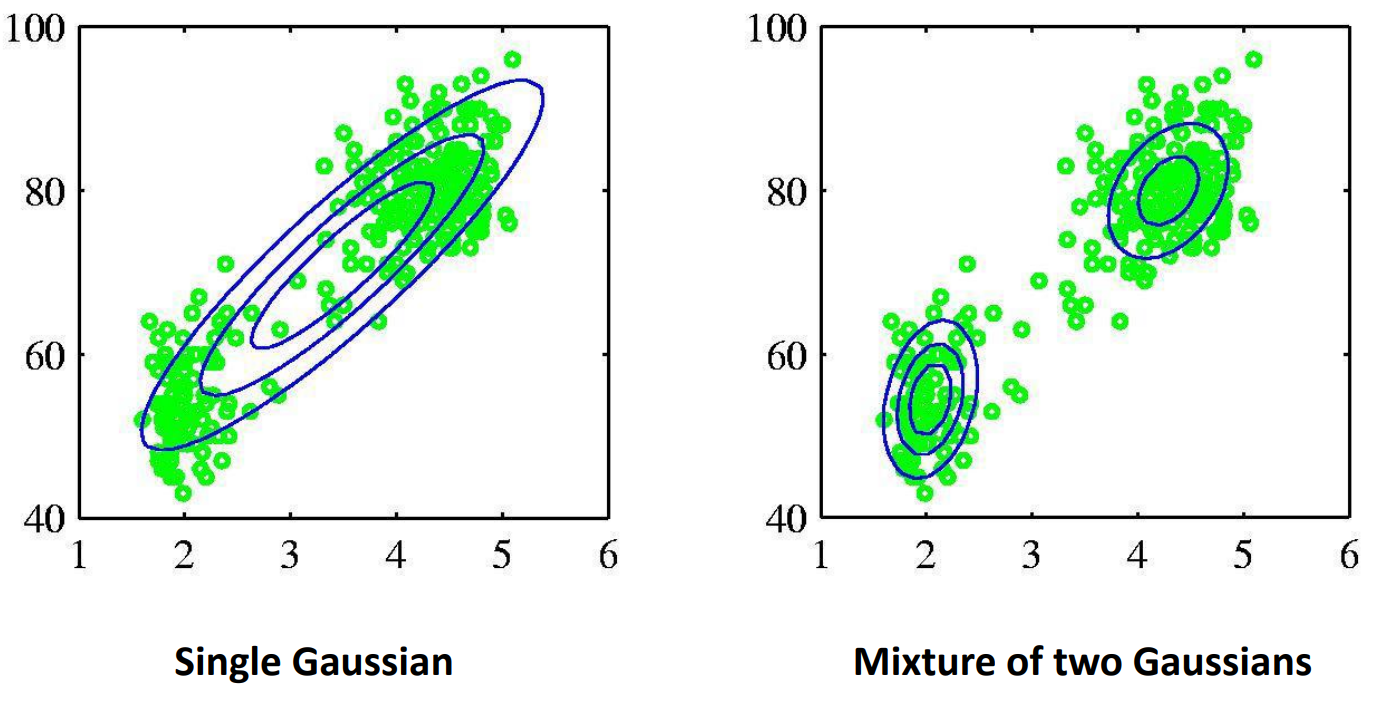
일반적인 gaussian 분포 즉, single gaussian 그림을 보면 본 데이터에 대한 분포를 설명을 잘 할 수가 없다. 하지만 gaussian을 두개 쓰면서 즉 Mixture of two Gaussian을 보면 해당 데이터셋을 잘 설명을 할 수 있다.
그러면 이러한 Mixture of Gaussian 의 형태는 어떻게 될까?
Mixture Gaussian은 Gaussian distribution을 여러개 붙인 것이다. 따라서 weight 값을 붙여져서 summation 한 것이 Mixture Gaussian이다.
따라서 Mixture Gaussian 의 형태는 다음과 같이 이뤄진다.
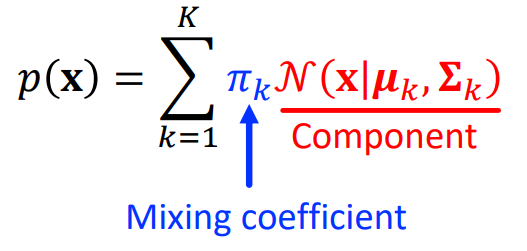
여기서 mixing coefficient는 모두 합했을 때 1을 가지는 weight 라고 생각하면 된다.
따라서 이러한 Gaussian distribution 3개를 합쳐보면 다음과 같은 형태를 띈다.
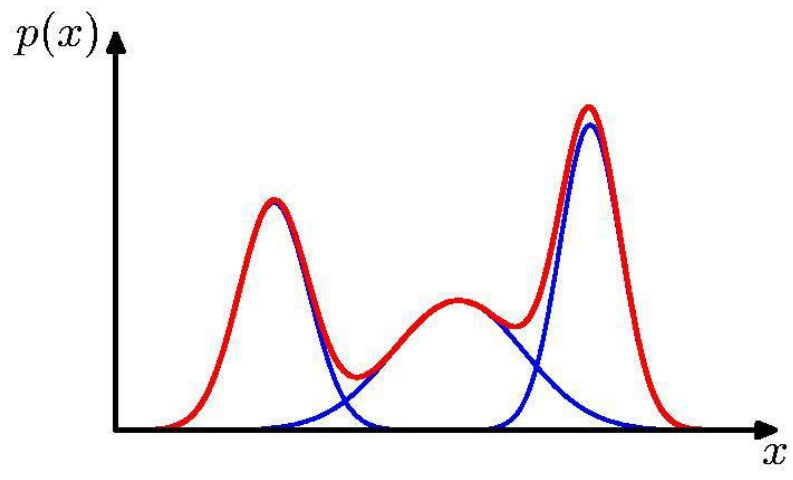
파란색이 일반 single gaussian distribution을 의미하고 빨간색은 이를 모두 합친 Mixture Gaussian을 의미한다.
그러면 이러한 Mixture Gaussian은 MLE를 어떻게 할까?
Mixture Gaussian은 기존의 Gaussian distribution과 다르게 \( \mu , \Sigma, \pi \)의 파라미터를 이용한다. \( \pi \)라는 파라미터 하나가 추가된 것이다. 여기서 \( \mu , \Sigma \)는 분포의 개수마다 있다는 것을 인지해야한다.
Loglikelihood를 먼저 구해보자
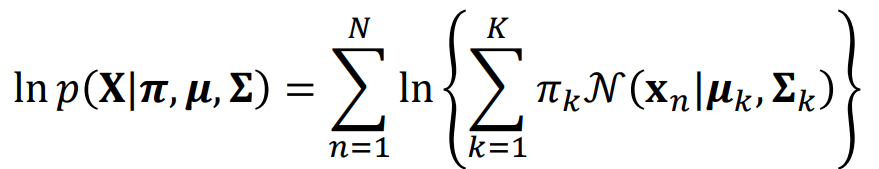
loglikelihood에 log를 취해준 형태는 다음과 같이 나온다. 하지만 우항에서 log식 안에 summation이 있는 형태는 closed한 maximum 값을 구할 수 없다. 즉, 미분이 불가능하다는 것이다. 따라서 이를 해결하기 위해 numeric optimization 방법 또는 EM 알고리즘을 통한 방법 등을 사용해야한다.
이러한 방법을 통해 MLE를 구하는 것은 추후에 다루도록 하겠다.