확률분포 정리

##  Uniform Distribution

특정 구간 내의 값들이 나타날 가능성이 모두 균등한 확률 분포를 의미

Uniform Distribution

$E(X)$	$\frac{1}{2}(a+b)$
$Var(X)$	$\frac{1}{12}(b-a{)}^2$

uniform distribution

 

##  Bernoulli distribution

확률 변수가 성공과 실패 두 결과 중 오직 하나로 나타나는 베르누이 시행의 결과에 대한 확률분포

성공과 실패의 2가지 경우만 존재

Bernoulli Distribution

$E(X)$	$p$
$Var(X)$	$p(1-p)=pq$

Bernoulli Distribution

 

##  Binomial distribution

Bernoulli 시행을 독립적으로 n번 반복했을 때 나타나는 결과에서 성공의 횟수에 관한 확률분포

$E(X)$	$np$
$Var(X)$	$np(1-p)=npq$

Binomial distribution

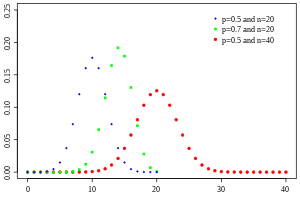
##  Negative Binomial distribution

성공 확률이 p, 실패확률이 1-p인 연속적인 베르누이 시행에서 x 번째 성공 전까지 실패 횟수

$E(X)$	$\frac{pr}{1-p}$
$Var(X)$	$\frac{pr}{(1-p{)}^2}$

##  Normal (Gaussian) distribution

평균 근처에서 확률 변수 값이 발생할 확률이 높고, 평균에서 멀어질수록 그 확률이 감소하는 종모양의 분포

Binomial Distribution을 정규근사

$E(X)$	$\mu$
$Var(X)$	${\sigma }^2$

표준 정규 분포 : $\mu$ = 0, $\sigma )$=1

$$Z=\frac{X-\mu }{\sigma }$$

##  Geometric distribution

성공의 확률이 p인 Bernoulli 시행을 독립적으로 반복하여 실시할 때 첫 성공이 나타날 때 까지의 실행 횟수에 대한 확률 분포

$E(X)$	$\frac{1}{p}$
$Var(X)$	$\frac{1-p}{p^2}$

 

##  Hypergeometric distribution

N개의 원소로 구성된 모집단에서 비복원 추출 방법에 의해 뽑혀진 표본에서의 확률분포

$E(X)$	$\frac{kM}{N}$
$Var(X)$	$\frac{kM}{N}(\frac{(N-M)(N-K)}{N(N-1)})$

 

https://losskatsu.github.io/statistics/hypergeometric/#1-%EC%B4%88%EA%B8%B0%ED%95%98%EB%B6%84%ED%8F%AC-%EC%A0%95%EC%9D%98

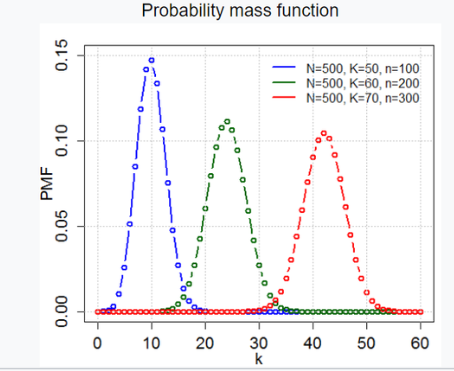
[기초통계] 초기하분포 의미 및 개념 정리

##  Multinoulli distribution

Bernoulli 시행의 확장으로 성공과 실패 2가지 경우가 아닌 3가지 이상의 경우로 시행한 결과의 분포

$E(X_i)$	$p_i$
$Var(X_i)$	$p_i(1-p)$

##  Multinomial distribution

Multinoulli 시행을 n번 반복하였을 때 각 결과가 특정 수만큼 나타날 확률에 대한 분포

$E(X_i)$	$n{p}_i$
$Var(X_i)$	$n{p}_i(1-p)$

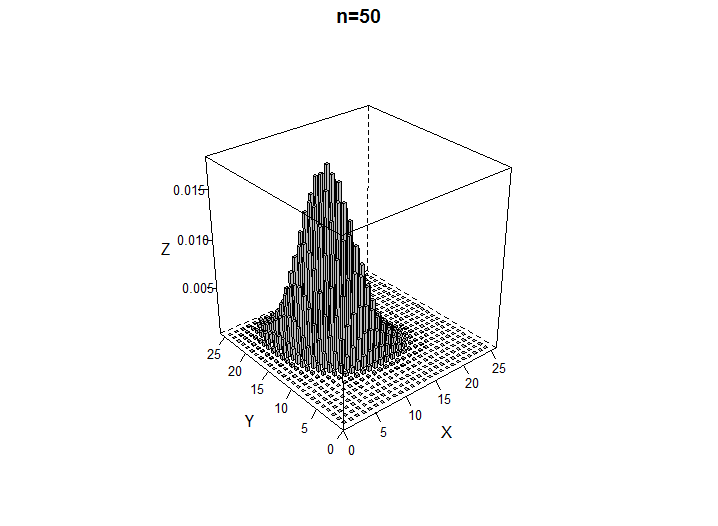
##  Poisson distribution

일정 기간에 희귀한 사건이 발생할 건수의 분포

$E(X)$	$\lambda$
$Var(X)$	$\lambda$

##  Exponential distribution

사건이 발생할 때(포아송분포를 따름) 지정된 시점으로부터 이 사건이 일어날 때 까지 걸린 시간을 측정한 확률분포

$E(X)$	$\frac{1}{\lambda }$
$Var(X)$	$\frac{1}{{\lambda }^2}$

Exponential Distribution의 무기억성(Memoryless property) : 어떤 시점부터 소요되는 시간은 과거 시간에 영향을 받지 않는다 (기하분포도 무기억성 가짐)

Proof of Memoryless property

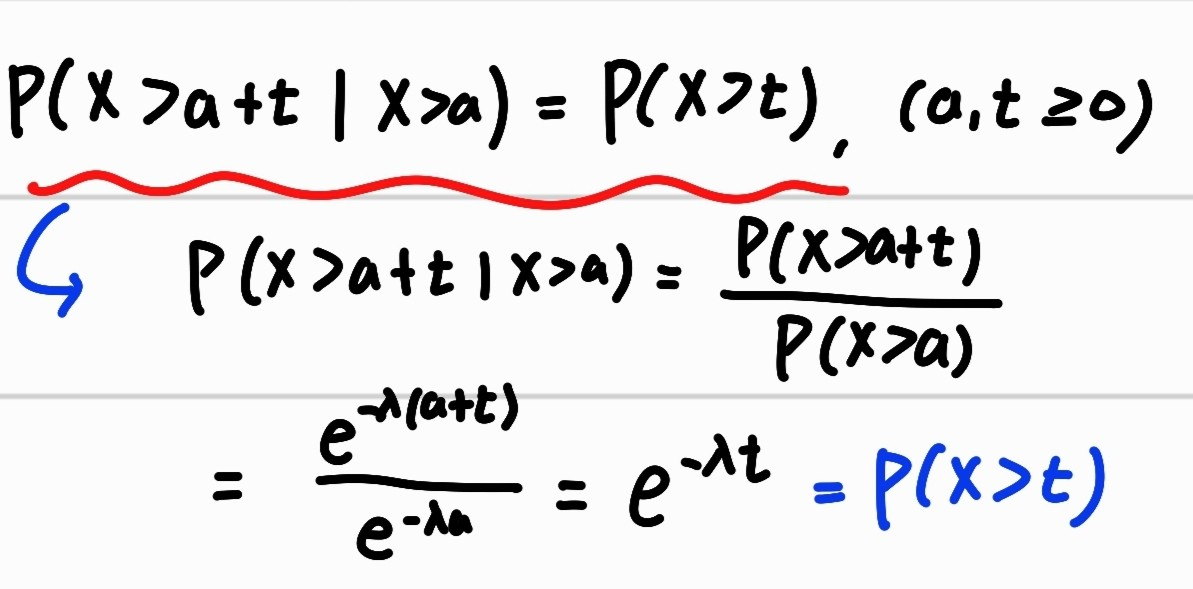
##  Gamma distribution

Exponential distribution은 한 번의 사건에 대한 시간을 측정한 확률 분포임에 반해 Gamma distribution은 여러 번의 사건이 나타날 때의 측정한 확률 분포.

즉, Exponential distribution은 gamma distribution의  $\alpha$가 1일 때를 의미

$\mathrm{\Gamma }(\alpha )=(\alpha -1)!$ , $\mathrm{\Gamma }(\alpha )=(\alpha -1)\mathrm{\Gamma }(\alpha -1)$ , $\mathrm{\Gamma }(\frac{1}{2})=\sqrt{\pi }$ 가 $\mathrm{\Gamma }$ 함수 공식

$E(X)$	$\alpha \beta$
$Var(X)$	$\alpha {\beta }^2$

##  Beta distribution

확률에 대한 확률분포. 베이지안에서 사전 분포로 쓰임

 모수에 따라 다양한 형태로 변형 가능하기 때문

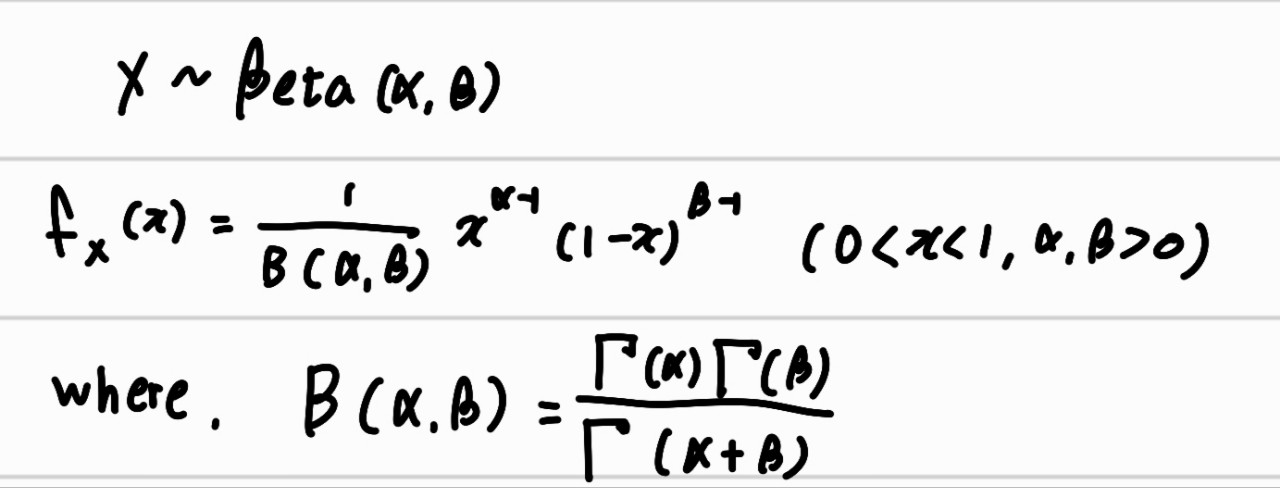
$E(X)$	\frac{\alpha}{\alpha + \beta}
$Var(X)$	$\frac{\alpha \beta }{(\alpha +\beta {)}^2(\alpha +\beta +1)}$

 

##  Distribution 관계도

distribution 관계

 

 

## Reference

https://soohee410.github.io/

Suri's Data Journal

https://losskatsu.github.io/statistics/betadist/#%EC%B0%B8%EA%B3%A0%EB%A7%81%ED%81%AC

[기초통계] 베타분포 의미 및 개념 정리

https://blog.naver.com/pwbrain/60049866617

[확률분포] 확률분포 정리