Information Theory의 핵심은 Entropy 이다.
## Entropy
Entropy는 불확실성을 측정하는 지표로 random variable에 대한 평균 정보량을 측정하는 것이다.
$$ H(x) = - \Sigma_{x} p(x) \ln p(x) $$
이를 자세히 설명하기 위한 예를 들어보겠다.
## Example
Question ) x가 8개의 state가 존재하는데 이를 전송하기 위해 x는 몇개의 bit가 필요할까?
8개의 가능한 bit는 \( \{ a,b,c,d,e,f,g,h \} \) 라고 하자. 그리고 이에 대한 각각의 확률은
\( \{ \frac{1}{2}, \frac{1}{4},\frac{1}{8},\frac{1}{16},\frac{1}{64},\frac{1}{64},\frac{1}{64},\frac{1}{64} \} \) 라고 하자.
이를 entropy 값을 구하면 필요한 bit 수가 나오게 된다. 계산의 편의상 ln 대신 \( log_2 \)를 써서 계산하면 다음과 같다.
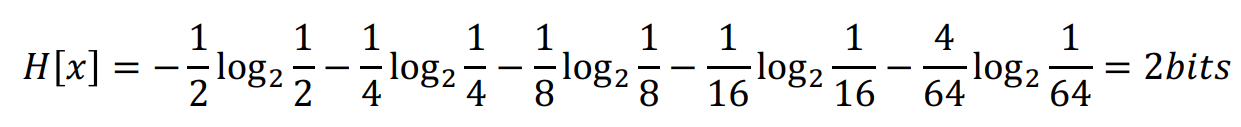
이를 entropy로 접근하는 것이 아닌 실제 coding theory에서 최소 코드 길이 할당하는 공식을 이용하여 계산해보자.
최소 길이 코딩은 \( -log_{2} p(x) \) 이다. 이를 각각 a~h 까지 계산해보면

다음과 같은 결과가 나오고 이에 대한 평균을 구해보면

다음과 같이 2 bit가 도출되는 것을 알 수 있다.
그러면 만약에 각각 다른 확률이 아닌 모두 확률이 \( \frac{1}{8} \)로 uniform distribution을 가지면 어떻게 될까?
바로 Entropy를 구하면
$$ H(x) = -\frac{8}{8}log_{2} \frac{1}{8} = 3 $$
로 3 bit가 도출된다.
따라서 uniform distribution을 따르는 확률이 entropy가 더 높아짐을 알 수 있다.
왜 높은지 불확실성 이라는 개념의 관점으로 해석해보자
단순 스포츠 도박의 확률로 비유하면 이해가 쉬워진다. A 라는 팀과 B 라는 팀의 경기가 있다고 하자.
A라는 팀의 승률은 95 % 이고, B라는 팀의 승률은 5% 라고 하자. 그러면 누가 이긴다고 돈을 베팅할 것인가.
당연히 A라는 팀이 승률이 높으니까 A 팀에 돈을 걸 것이다(역배 제외). 그러면 이 경기는 불확실성이 높은 경기인가?
A라는 팀이 이길 확률이 높으므로 불확실한 경기가 아니다.
그러면 C 팀과 D 팀은 서로 승률이 둘다 50% 라고 하자. 그러면 이 경기는 어디에 베팅을 걸 것인가? 이는 불확실성이 높은 경기인가?
당연히 C랑 D 중 어디가 이길지 매우 불확실하기 때문에 이는 불확실성이 높다.
따라서 이를 확률 분포로 보면 Uniform distribution은 확률이 모두 같은 경우를 의미하므로 매우 불확실성이 높은 distribution이라고 할 수 있다.
## Entropy Analysis

다음과 같은 histogram을 보면서 생각해보자. M개의 bin으로 하여 나눠보자. 그리고 \( \Sigma_{i}^{M} n_{i} = N \) 이라고 해보자.
그러면 여기서 다양성(Multiplicity) W를 구할 수 있다.
$$ W = \frac{N ! }{\Pi_{i}n_{i} !} $$
Entropy의 식을 보면 다양성과 연관이 있음을 알 수 있다. Entropy H는 다양성에 log를 취해준 것과 동일하다.
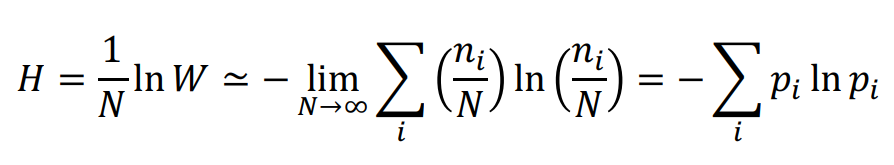
따라서 이러한 식에서 maximize 하는 \( p_i \)를 보면 \( \frac{1}{M} \)이 된다. 즉, uniform distribution을 따를 때 Entropy는 최대화된다.

그럼 지금까진 discrete 한 경우만 알아봤는데 continuous 한 경우는 어떨까? 간단하다. \( \Sigma \) 가 아닌 \( \int \)로 해주면 된다.
$$ H(x) = \int p(x) \ln p(x) dx $$
그러면 이를 기반해서 Gaussian distrbution( \( \mathcal{N}(x| \mu , \sigma^{2} \) ) 일 때, Entropy를 구하면
$$ H(x) = \frac{1}{2} \{ 1 + \ln (2 \pi \sigma^2 ) \} $$
가 된다.
그리고 conditional entropy와 joint entropy를 각각 구하면
$$ H[y|x] = - \int \int p(x,y) \ln p(y|x) dx dy $$
$$ H[x,y] = H[y|x] + H[x] $$
와 같다.
## Relative Entropy
우선 실제 데이터의 분포 p(x) 를 정의한다. 하지만 우리는 실제 데이터의 분포를 모른다.
그래서 이에 근사하는 분포 q(x)를 정의한다. 따라서 이러한 q(x)의 분포를 p(x)와 비슷하게 만드는 것이 목적이다. 즉 p(x)와 q(x)의 차이가 가장 작아지게 만드는 것이다. 따라서 이 p(x)와 q(x)의 차이가 relative entropy 이다.

따라서 q(x)에 기반한 근사하는 entropy 값에 실제 entropy 값을 빼줌으로써 KLD 공식이 나오게 된다.
이러한 KLD의 특징에 대해서 알아보면
첫째로 교환 법칙이 성립하지 않는다는 것이다. \( KL(p||q) \neq KL(q||p) \)
두번째로 KLD는 무조건 0보다 크거나 같다는 것이다. \( KL(p||q) \geq 0\)
마지막으로 p에 속한 sample 들에 대해서 KLD를 계산하는 것은
$$ KL (p||q) \simeq \frac{1}{N} \Sigma_{n=1}^{N} \{ -\ln q (x_n | \theta) + \ln p (x_n ) \} $$
와 같이 된다. 여기서 실제 값 \( x_n \) 에 대해서 모르기 때문에 \( -\ln q (x_n | \theta) \)를 최대화 또는 최소화를 시킨다.

교환 법칙 성립이 안되는 것에 대해서 보면
오른쪽은 KL(p || q) 이고 왼쪽은 KL(q||p) 이다.
q는 p에 근사하게 Gaussian distribution을 기반으로 생성된다. 따라서 forward KLD는 p(z)를 기준으로 만들어지기 때문에 오른쪽 그림처럼 분포가 형성되고 반대로 왼쪽은 p(z)를 모두 포함하는 형태로 분포가 형성된다. 따라서 q는 \( \mu \)와 \( \sigma \)의 조절로 q 분포를 형성한다.
따라서 두 분포의 순서를 바꾸면 q의 분포가 달라지므로 KLD도 달라지게 된다.
## Mutual Information
Mutual information은 두 분포의 독립성을 측정하는 것이다.
두 분포 p(x)와 p(y)에 따른 식은 다음과 같다.
$$ I(x,y) = KL(p(x,y) || p(x)p(y) ) = - \int \int p(x,y) \ln (\frac{p(x) p(y) }{p(x,y)}) $$
이러한 mutual information은 다음과 같은 특징을 갖는다.
Mutual information은 \( I(x,y) \geq 0 \) 이다.
\( I (x,y) = 0 \) 이면 \(p(x,y) = p(x)p(y) \) 이고 이에 대한 역도 성립한다. (독립이다)
\( I(x,y) = H(x) - H(x|y) = H(y) - H(y|x) \) 이다.
'Probability & Statistics' 카테고리의 다른 글
| Nonparametric method (0) | 2022.08.03 |
|---|---|
| Probability Distribution (0) | 2022.08.02 |
| Decision Theory (0) | 2022.08.01 |
| Probability Theory (0) | 2022.07.31 |
| 확률분포 정리 (0) | 2022.07.17 |




댓글