## Decision Theory
decision theory는 한마디로 정의하자면 어떻게 하면 올바른 선택을 할 수 있을까라는 것에 대한 이론이다.
decision theory는 2가지 step으로 나뉜다.
1. inference step : training data x의 Posterior distribution \( p(C_k | x )를 구하는 것
2. 이를 기반으로 x가 주어지면 최적의 t를 구한다.
여기서 x는 현재 데이터 , t는 예측 데이터이다.
예를 들면 x를 현재 주식시장의 상황이라고 하고 t를 매수 또는 매도라고 하자. 만약에 과거의 최적의 매수 매도 타이밍을 안다고 가정하면 이를 기반으로 확률 분포 p(t|x) or p(x,t)를 구할 수 있다. 따라서 이러한 분포를 기반으로 새로운 데이터 x'이 주어질 때 매수해야되냐 매도해야되냐를 결정하는 것이다.
## Decision Theory Problem Example
또 다른 문제상황을 정의하자. x는 X-ray 이미지라고 하고, 이에 따른 결정 즉 Case 1 = 암에 걸렸다, Case 2 = 암에 걸리지 않았다 라고 하자.
이를 region으로 재정의 해보자. 만약에 x가 Region 1 에 있으면 ( \( x \in R_1 \)) 암에 걸린 것이고, Region 2에 있으면 ( \( x \in R_2 \)) 암에 걸리지 않은 것이다.
그러면 이에 따른 오진율을 구하면

이와 같이 된다.
이 식을 해석하면 x가 R1 영역에 있는데 case 2로 예측할 확률 (joint) 과 x 가 R2에 있는데 case 1으로 예측할 확률을 더한 것이다. 따라서 이러한 오진율을 구할 수 있는 방법은 Region을 찾는 것이다. 이를 찾는 방법은 p(mistake) 확률을 줄이는 방향으로 학습을 하면 각각의 region을 찾을 수 있다.
이를 그림으로 표현하면
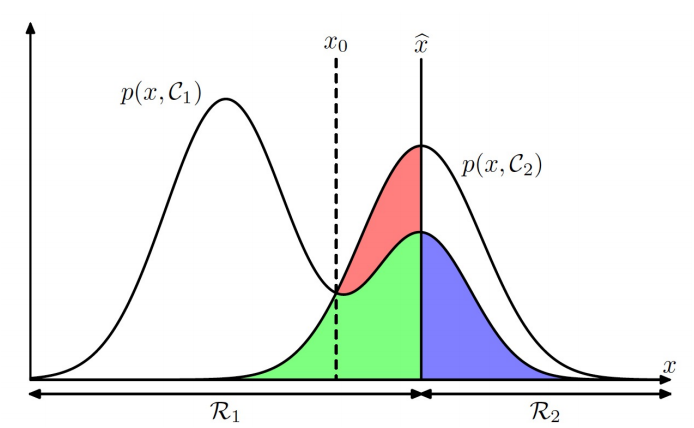
이와 같이 그려진다.
이 그림을 해석하자면 x 축에 쓰여있는 것과 같이 Region이 나눠져 있고 이를 구분하는 이상적인 경계값은 \( \hat{x}\) 가 된다. 하지만 처음부터 \( \hat{x}\)를 알지 못하므로 그림처럼 임의의 경계값 \( x_0 \)로 설정하고 이를 줄이는 방향으로 학습을 하여 Region을 구분한다.
하지만 이렇게 오진율을 줄이면서 학습하여 최적의 결정을 하는 것은 충분하지 않다.
왜냐하면 오진의 두가지 케이스를 다시 한 번 봐보자.
C1 : 암에 걸린 사람을 정상으로 판단하는 경우, C2 : 정상적인 사람을 암에 걸렸다고 판단하는 경우
이렇게 두가지 케이스 중 어떤 것이 오진을 했을 때 치명적일까? 바로 C1이다. 따라서 오진의 종류에 따라서도 무게가 다르므로 새로운 loss function을 정의한다.

위 식에서 L의 case를 보자.
1. 암에 걸린 사람한테 암에 걸렸다고 진단하면 loss는 0
2. 정상인 사람한테 정상이라고 진단하면 loss 는 0
3. 정상인한테 암에 걸렸다고 진단하면 loss는 1
4. 암에 걸린 사람한테 정상이라고 진단하면 loss는 1000
이렇게 weight를 경우에 따라서 다르게 주는 것이다.
따라서 이렇게 weight를 다르게 주면서 loss를 최소화 시킨다. 이렇게 최소화 하는 과정을 통해서 region을 나눌 수 있는 최적의 경계값을 구한다.
## Reject option
하지만 치명적인 loss 라는 것은 누가 어떻게 결정하는지에 따라 주관적이다.
따라서 Decision Theory에서는 이를 고려한 "Reject Option" 을 고려한다.
이 reject option을 한마디로 정의하자면 결정하기 어려운 상황은 결정을 피해라 이다.
이러한 것을 그림으로 나타내면 다음과 같다.
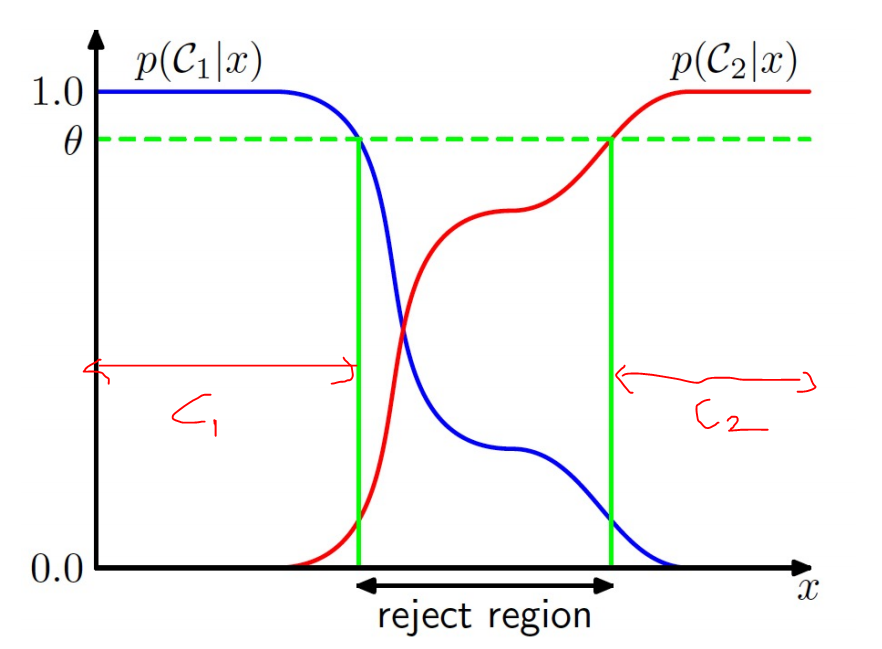
따라서 확실하게 C1 구간 C2 구간이라고 구분되지 않는 영역을 reject region 이라고 한다. 그림에서는 가운데가 reject region이다.
이러한 reject region을 설정하는 이유는 결정에 대한 error율을 줄이기 위함이다.
## Kinds of Decision approach
1. Generative models
Generative model은 거의 VAE를 생각하면 된다. 이는 Bayes' rule에 기반한다.
우선 class condition의 밀도 \( p(x|C_k ) \) 즉 likelihood를 결정한다. 그 다음으로 Piror 의 분포( \( p(C_k) \)) 를 구한다.
그리고 bayes' rule에 기반해서 Posterior를 구해 결정을 내린다.
2. Discriminator models
이는 처음부터 Posterior 확률을 구한다. 그리고 이를 통해 판단을 내린다.
즉, 1번에서 나온 Posterior를 통해 2번에서 결정을 하는 것이다.
Generative model과 Discriminator model의 차이는 우선 Generative model은 Bayes' rule을 이용하여 Posterior 를 구하는 것이고 Discriminator는 바로 Posterior를 구하는 것이다.
'Probability & Statistics' 카테고리의 다른 글
| Nonparametric method (0) | 2022.08.03 |
|---|---|
| Probability Distribution (0) | 2022.08.02 |
| Information Theory (0) | 2022.08.01 |
| Probability Theory (0) | 2022.07.31 |
| 확률분포 정리 (0) | 2022.07.17 |




댓글