본 포스팅에선 Probability Distribution 중 Parametric method에 대해 다뤘다.
2022.08.02 - [Probability & Statistics] - Probability Distribution
Probability Distribution
간단한 요약 버전은 2022.07.17 - [Probability & Statistics] - 확률분포 정리 확률분포 정리 ## Uniform Distribution 특정 구간 내의 값들이 나타날 가능성이 모두 균등한 확률 분포를 의미 \( E(X) \) \(\frac..
bigdata-analyst.tistory.com
Nonparametric method는 확률의 어떠한 특정한 형태가 있는 것이 아닌 데이터에 기반해서 분포를 구하는 방법이다. 이러한 기법 중 가장 대표적인 것이 histogram이다. histogram은 어떠한 형태를 미리 정의한 것이 아니라 데이터의 개수에 따라서 형성되므로 Nonparametric method라고 할 수 있다.
그리고 앞선 포스팅에서 강조하였던 Conjugate Prior 에 대해서 다시 리뷰한다.
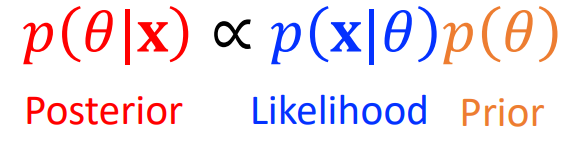
일반적으로 바로 Posterior를 구하는 것은 쉽지가 않다. 따라서 이를 해결하기 위해 Likelihood를 특정 분포를 따르게 한다. 그리고 Prior distribution과 Posterior distribution을 같은 분포로 설정하면 문제를 쉽게 해결할 수 있다.
따라서 한마디로 정의하면 Likelihood가 특정한 분포를 따를 때, Prior 분포와 Posterior 분포를 같게함으로써 좀 더 쉽게 Posterior를 구할 수 있는 방법이다.
각 Likelihood가 특정 분포를 따를 떄에 Prior 분포를 어떻게 설정해야할지에 대한 표는 다음과 같다.

## Nonparametric Method (Histogram)
Parametric method와 Nonparametric method에 대해 간단히 알아보면 Parametric method는 확률모델 p에 대해 많은 제약을 주면서 특정한 형태를 띄게 만든다. 반면에 Nonparametric method는 확률 모델 p에 가능한한 제약을 주지 않고 data 분포에 대해 p가 모델링 되는 것이다.
대표적인 Nonparmeteric method인 histogram에 대해 먼저 알아보겠다.
histogram을 생각해보면 bin의 개수(나누는 개수)와 폭의 넓이에 따라서 데이터를 다르게 표현할 수 있다.

histogram은 다음과 같이 수학적으로 영역에 해당하는 확률을 표현할 수 있다.
$$ p_i = \frac{n_i}{N \Delta_i} $$
여기서 \( \Delta_i \)는 넓이이고, \( n_i \)는 bin 값을 의미한다. 그리고 N은 데이터의 개수를 의미한다. 그림에서도 볼 수 있듯이 \( \Delta \) 값이 작이질수록 histogram이 원래의 분포를 잘 반영할 수 있게 된다. 또한, bin 즉 n이 커질수록 원래분포를 잘 반영할 수 있다.
하지만 \( \Delta \) 값이 작아지면 작아질수록 고려해야 할 개수가 많아져서 curse of dimension의 문제로 이어질 수도 있다. 따라서 \( \Delta \) 값을 적당히 설정해야된다.
그러면 이러한 histogram의 확률과 개수 등은 어떻게 구할까
histogram의 확률은 간단하다. 내가 관심있는 영역을 R (Region) 이라고 하였을 때 그 Region R에 대한 확률은
$$ P = \int_{R} p(x) dx $$
로 표현할 수 있다.
그리고 해당 영역 R에 있는 관측치 개수를 구하는 식은 다음과 같다.
$$ K \simeq NP $$
R에 있는 관측치 개수는 N이 커질 때 N과 R의 확률을 곱한 것과 같다는 것이다.
그리고 R에 있는 지역의 부피를 V라고 했을 때 확률 P는 각 histogram 하나의 확률 p(x)와 V로 나타내질 수 있다.
$$ P \simeq p(x)V $$
그럼 이는 p(x)를 \( \frac{K}{NV} \)로 표현할 수 있다.
## Kernel Density Estimation
kernel density estimation 은 histogram에서 도출한 \( p(x) = \frac{K}{NV}\)에서 분모인 NV를 고정하고 K를 estimation하는 것이다.
K는 지역 R에 있는 data의 개수임을 다시금 상기한다.
Kernel Density Estimation 방식은 다음과 같은 그림처럼

여기서 빨간점은 실제 data이고 파란점은 hypercube의 중심점이다. 따라서 kernel density estimation은 실제 데이터에 대해 폭 h를 갖는 hypercube를 정한다 따라서 이러한 차이를 계산해서 추정한다.
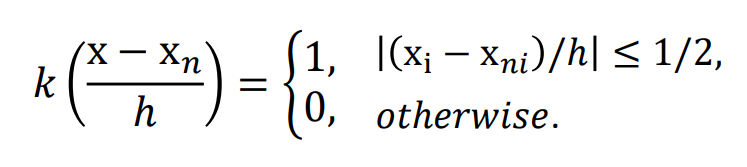
즉 이 식에서 \( x_i \)는 hypercube의 점 즉 파란색, \( x_{ni} \)는 데이터 빨간색 점을 의미한다.
따라서 이렇게 \( k \frac{x - x_n}{h}\)를 구하고 이를 모두 summation 해줌으로써 K를 추정한다.
따라서 Kernel Density Estimation에서는 p(x)를 \( \frac{K}{NV} \)로 정의하는 것이 아닌 \( \frac{\Sigma_{n=1}^{N}k \frac{x - x_n}{h}}{Nh^D} \) 로 정의한다. 이 때, hypercube를 정하는 함수 k를 kernel function이라고 한다.
정리하자면 확률 p(x)를 K를 kernel function을 이용하여 근사화를 하여 구한 것이 kernel density estimation이다.
하지만 실제에서는 hypercube 형태가 아닌 gaussian 형태를 가지게 kernel function을 설정한다. 따라서 p(x)는 다음의 식을 따른다.

따라서 다음 그림은 guassian kernel function을 이용하여 p(x)를 추정한 형태이고 이는 gaussian의 폭 h 값에 의해서 달라진다. h가 크면 매우 smoothing 하게 예측을 하고, h를 작게하면 너무 noise 값이 있는 것 처럼 예측하게 된다.
## Nearest Neighbor Density Estimation
앞서 살펴본 Kernel Density Estimation은 NV를 고정하고 K를 근사해서 예측하는 형태였다면, Nearest Neigbor Density Estimation은 K를 고정하고 V를 예측하여 근사화시키는 것이다.
이러한 경우 하나의 test point를 잡고 이를 기준으로 설정한 영역 안에 데이터들이 몇개가 들어있는지를 예측하는 것이다.
따라서 이 또한, K의 개수에 따라서 distribution을 예측하는 것에 매우 영향을 받고 K 값에 따른 예측은 다음 그림과 같다.

이러한 Nearest Neighbor 방법은 Density 목적보단 classification 목적으로 자주 쓰인다. 자주 들어본 KNN 방법의 기초이다.

그림과 같이 하나의 test point를 정하고 이에 가까운 점이 어떠한 class에 있는지를 예측하여 구분선을 생성한다.
따라서 이러한 K의 개수에 따라서 KNN classification을 한 visualization이다.
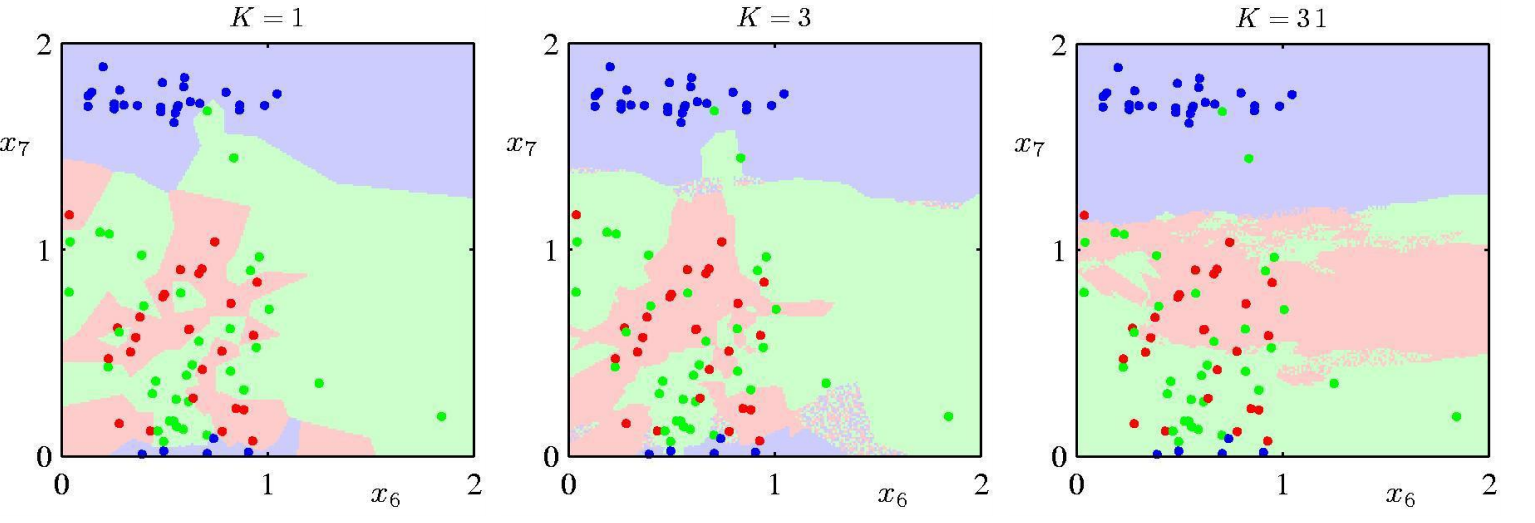
K가 작으면 매우 정교하게 구분을 하고 (Overfitting) , K가 매우 크면 매우 뭉뚱그려서 분류(Underfitting)를 하는 것을 볼 수 있다.
'Probability & Statistics' 카테고리의 다른 글
| Linear Regression (0) | 2022.08.05 |
|---|---|
| Probability Distribution (0) | 2022.08.02 |
| Information Theory (0) | 2022.08.01 |
| Decision Theory (0) | 2022.08.01 |
| Probability Theory (0) | 2022.07.31 |




댓글