유명한 알고리즘인 Red Black Tree에 대해서 알아보자
복잡도는 다루지 않을 것이며 삽입 과정만 다루겠다
Red Black Tree를 이해하기 위해선 2-3-4 트리의 이해가 우선적으로 되어야지 조금 쉽다. 왜냐하면 2-3-4 트리의 단점을 극복하기 위해 제안된 것이 Red-Black Tree 이기 떄문이다.
Red = 다수의 노드, black은 보통 이라고 임의로 정의한다
Red Black Tree는 3가지 핵심 규칙이 있다.
1. Root node는 모두 black이다.
2. Root에서 외부노드(끝)까지의 경로 상에는 연속된 2개의 Red node가 포함되지 않는다.
3. 루트에서 각 외부 노드까지의 경로에 있는 Black node의 수는 모두 같다.
그리고 Red-Black Tree는 Binary Search 알고리즘을 기본으로 하고 있다는 것을 알아야한다.
Red Black Tree 에서 가장 핵심은 색 변환과 회전이다.
먼저 색 변환에 대해서 알아본다.
## 색 변환
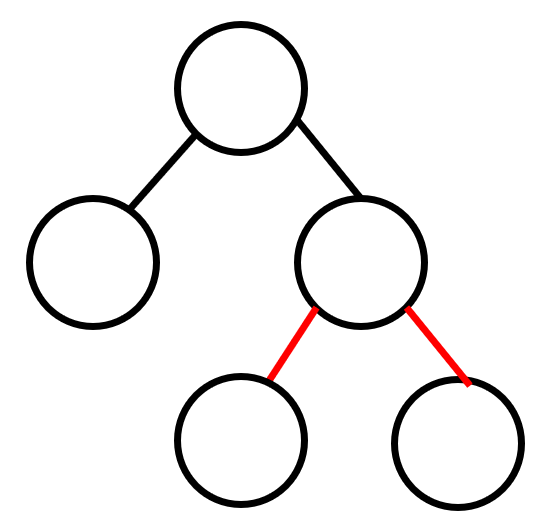
이렇게 노드가 구성될 때, 만약 새로운 노드가 들어오면 다음과 같이 변한다.
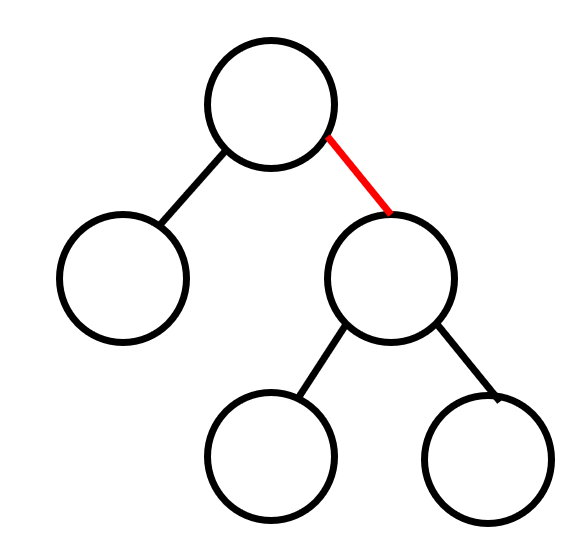
두 개의 레드 링크가 상위의 링크가 레드 링크로 변환된다.
예를 들어 보자. [2,1,8,9] 가 차례대로 들어온다고 가정하자. 다음과 같은 과정을 거치게 된다.

처음은 루트노드여서 black이고 나머지는 들어올 때 red 로 들어온다고 생각하면 된다. 그래서 1은 2보다 작으니 왼쪽, 8은 2보다 크니 오른쪽으로 레드-레드가 되고, 그 다음 9가 들어올 땐 우선적으로 양 쪽에 있는 red 색깔을 블랙으로 바꾼다. 여기서 부모노드가 root 노드이니 상위 노드가 없으므로 그대로 블랙으로 변환이되고 9가 삽입된다.
## 회전
- 단순 회전

이와 같은 경우는 2법칙에 알맞지 않다. 따라서 이는 회전을 통해 변환시켜줘야한다. 다음과 같이 변환된다.
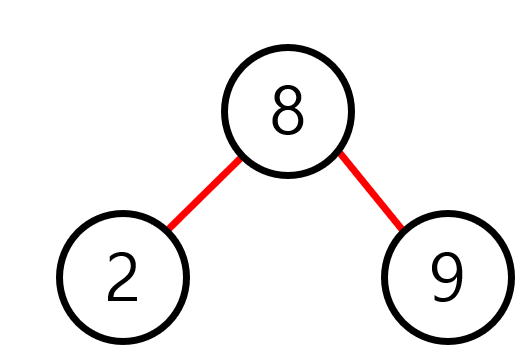
보이는 것처럼 가운데 값을 위로 끌어올려 왼쪽에 상위 노드를 오른쪽엔 자식 노드로 구성하는 것이다. 이 때, 레드 트리는 유지된다.
이것도 예시로 한 번 알아보자. [1,2,3,4] 를 예시로 든다.

이처럼 숫자가 2가 루트노드로 가서 1,3을 자식노드로 갖게 되고 그 다음에 색깔이 black으로 바뀐 후, 4가 삽입된 것을 볼 수 있다.
- 이중 회전

이런 경우는 어떻게 처리할까? 이런 경우에는 두번의 회전 과정이 필요하다. 첫번째로는 한줄로 펼쳐주는 과정이 필요하다. 이 때, 맨 밑의 노드가 그 위의 상위 노드보다 크기 때문에 9-2-8 인 순서를 9-8-2의 순서로 바꿔야한다. 그 다음에는 단순 회전과 같은 형태로 풀어나가면 된다.
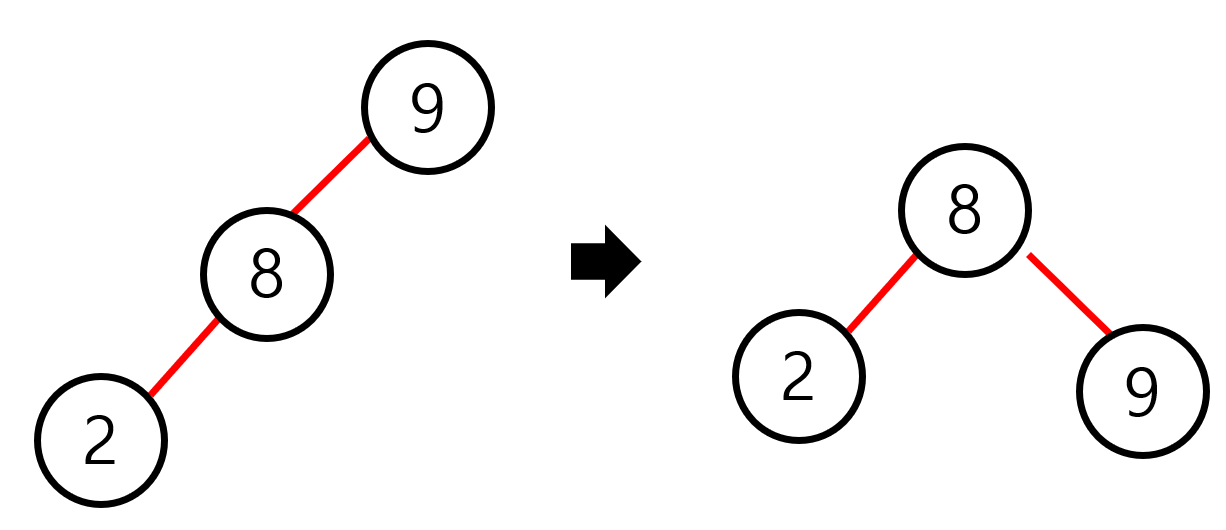
바로 예시로 넘어가보자. 아까 했던 [2,1,8,9]에 이어서 [7,3,6] 을 추가로 삽입해보자
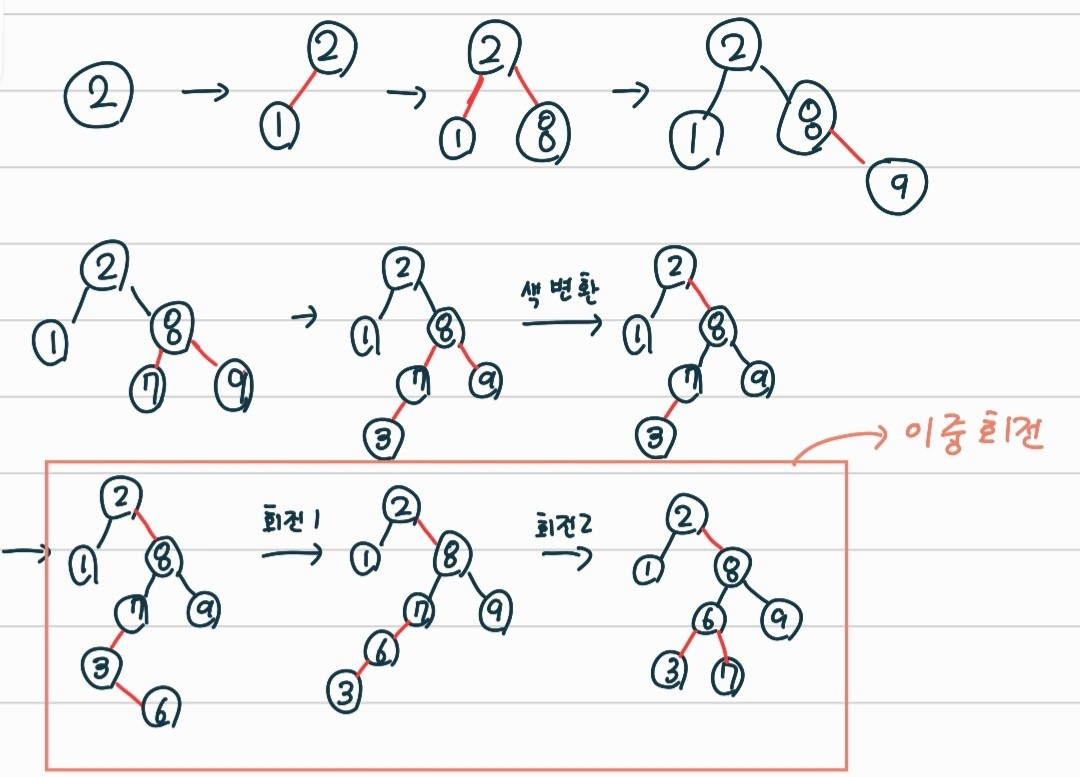
7-3-6 에서 회전이 일어나고 또 다시 회전이 일어나는 것을 볼 수 있다.
여기서 중요한 점은 uncle 노드 즉, red 의 옆쪽에 있는 노드가 black이 아니라 red 이면 이중회전은 일어나지 않는다. 이 땐 색변환만 일어난다.

# 응용 문제
[8,9,7,3,6,4,5,1,2] 를 삽입하였을 때 레드블랙 트리의 구조는?
그리고 이중회전이 첫번째 일어나는 부분은 어디인가?

이중 회전과 색 변환이 모두 들어가 있는 예시여서 알맞다고 생각한다.
그리고 나중에 자기만의 예시를 하고 확인할 때
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
이 사이트를 참고하면서 확인하면 좋다.
Red Black Tree 코드는 https://github.com/winston1214/INU/blob/master/algorithm/5week/redblacktree.py
GitHub - winston1214/INU: Summary of INU classes
Summary of INU classes. Contribute to winston1214/INU development by creating an account on GitHub.
github.com
'자료구조' 카테고리의 다른 글
| 버블 정렬(Bubble Sort) (0) | 2021.10.22 |
|---|---|
| 선택 정렬 (0) | 2021.10.22 |
| Linked List - C와 Python 비교 - 개념 (1) | 2020.07.15 |
| queue - 3 (0) | 2020.07.15 |
| Queue - C와 Python 비교 - 2 (0) | 2020.07.13 |




댓글