본 글은 https://www.youtube.com/watch?v=OnZIDatotZ4 이 동영상을 참고하여 작성하였습니다.
RAFT는 ECCV2020에서 베스트 논문상을 받은 논문이다. Optical Flow와 Transformer를 결합하면서 SOTA를 달성한 논문이다.
RAFT는 엄청난 성능을 보이면서 SOTA를 달성하는 Contribution을 주는 네트워크이다.
RAFT에 대해 설명하기 전에 Optical Flow의 dataset에 대해서 간단하게 알아보겠다.
Flying Chair와 Flying Things 같은 경우는
FlowNet : Learning Optical Flow with Convolutional Networks(Optical Flow~FlowNet2.0)
본 글은 https://www.youtube.com/watch?app=desktop&v=Z_t0shK98pM 기반으로 작성되었습니다. ## Optical Flow란? Optical Flow는 연속한 두 Frame 사이에서 각 Pixel의 Motion을 타나내는 Vector Map이다. 그림..
bigdata-analyst.tistory.com
이 포스팅을 참고하면 될거 같다.
이번에 소개할 Dataset은 MPI-Sintel이다. 이 MPI dataset은 sintel이라는 영화에 나오는 동영상 이미지를 통해서 만든 데이터셋이다. 다음에 소개할 KITTI dataset과 더불어 보통 train용이 아닌 test 용으로 사용을 많이 한다.

이 데이터셋은 optical flow 뿐만 아니라 GT occlusion도 나와있다.
다음은 KITTI dataset이다. KITTI dataset은 보통 자동차의 주행 영상을 찍은 데이터셋이다. 하지만 KITTI dataset 같은 경우 optical flow에 대한 gt 이미지가 매우 적은 단점이 있다.

들어가기에 앞서 기존의 Supervised Learning으로 Optical Flow를 Estimation 한 것에 대해 알아보겠다.
## Supervised Learning Optical Flow Estimation
### PWC-Net(CVPR2018)
PWC-Net에서 P는 Pyramid, W는 Warpping, C는 Cost Volume(Corrleation Volume)을 말한다.

### SpyNet(CVPR2017)
SpyNet에서 처음으로 spatial pyramid network라는 구조를 처음 제안하였다.
기존의 FlowNet은 input image를 concat해서 inference 한 번을 거쳐서 optical flow를 바로 뽑아내는 구조였다면, SpyNet은 DownScaling을 하고 제일 작은 scale에서 optical flow를 구한다. 그리고 이를 기반으로 하여 다음 scale에서의 optical flow를 계산하고 이 과정을 반복한다.

이렇게 계층적으로 Optical Flow를 계산하게 된다.
이러한 방법을 사용하면 Large Motion에 대한 계산을 용이하게 할 수 있게 된다.
### Warping(Backward Warping)
warping operation은 optical flow가 있을 때 이미지를 optical flow에 따라서 움직이는 연산이다.
그림에서 \(F_{12}\)는 \(I_{1}\)과 \(I_{2}\)의 optical flow이다. 이 때 pixel 별로 optical flow에 대해서 정해진다.
그리고 \(I_{2}\)에 있는 pixel 들을 \( \hat{I_{2}} \) 에 매핑을 시킨다. 따라서 식은 다음과 같이 이뤄진다.
$$ \hat{I_{2}}(x) = I_{2}(x+F_{12}(x)) $$
이러한 식으로 픽셀 값들을 다시 갖고 와서 새로운 이미지를 만드는 것이다. 이렇게 만들어진 \( \hat{I_{2}} \) 는 \(I_{1}\) 시점으로 \( I_{2}\)를 옮긴 버전인 것이다.
그리고 \(I_{1}\)과 \( \hat{I_{2}} \)는 항상 같지 않은데 이는 occulusion 같은 문제로 인하여 \(I_{1}\)에 없었던 이미지(ex. 바위)가 생길 수 있기 때문이다.

이러한 warping 기법은 주로 inference한 flow를 중간에 warping operation 사용하여 그 warping된 이미지를 같이 사용하여 inference를 하는 방법을 이용한다.
warping을 할 때 픽셀이 정수 단위가 아니라 float 단위로 나타나게 될 수도 있다. 이럴 땐 bilinear interpolation을 통하여 픽셀을 추출한다. 이러한 방법은 임의의 어떤 점이 있더라도 연속적으로 가져갈 수 있다는 것이 장점이다. 또한 이러한 pixel들은 미분도 가능하단 장점이 있다.
### Cost Volume(Correlation Layer)
FlowNet에서 Corrleation Layer 부분을 참고하면 된다.
FlowNet : Learning Optical Flow with Convolutional Networks(Optical Flow~FlowNet2.0)
본 글은 https://www.youtube.com/watch?app=desktop&v=Z_t0shK98pM 기반으로 작성되었습니다. ## Optical Flow란? Optical Flow는 연속한 두 Frame 사이에서 각 Pixel의 Motion을 타나내는 Vector Map이다. 그림..
bigdata-analyst.tistory.com
## RAFT Network Architecture
RAFT 알고리즘은 전통적인 Optical Flow를 구하는 방식 중 Energy Minimization 방식을 차용하였다고 한다.
Energy Minimization이란 딥러닝으로 쉽게 말하자면 Global Minimum 값을 찾는 것이다.
$$ I(x,y,t) = I(x+u,y+v,t+1) $$
위와 같은 optical flow constraint를 Energy function으로 두어 이 값을 최소로 하기 위해 노력해왔다. 따라서 이러한 방식을 차용하여 RAFT 알고리즘은 Iteration 방법을 사용하였다.
이러한 Energy Minimization을 하기 위해 기존엔 Data Term 과 Regularization Term 을 고려하여 최적화를 하였다.
- Data Term은 t 프레임에서의 한 좌표와 t+1 프레임에서 움직였던 한 좌표의 픽셀은 같아야 한다는 것이다.
- Regularization Term은 한 그리드에서 주변의 optical flow는 서로 비슷할 것이라는 전제조건이다.
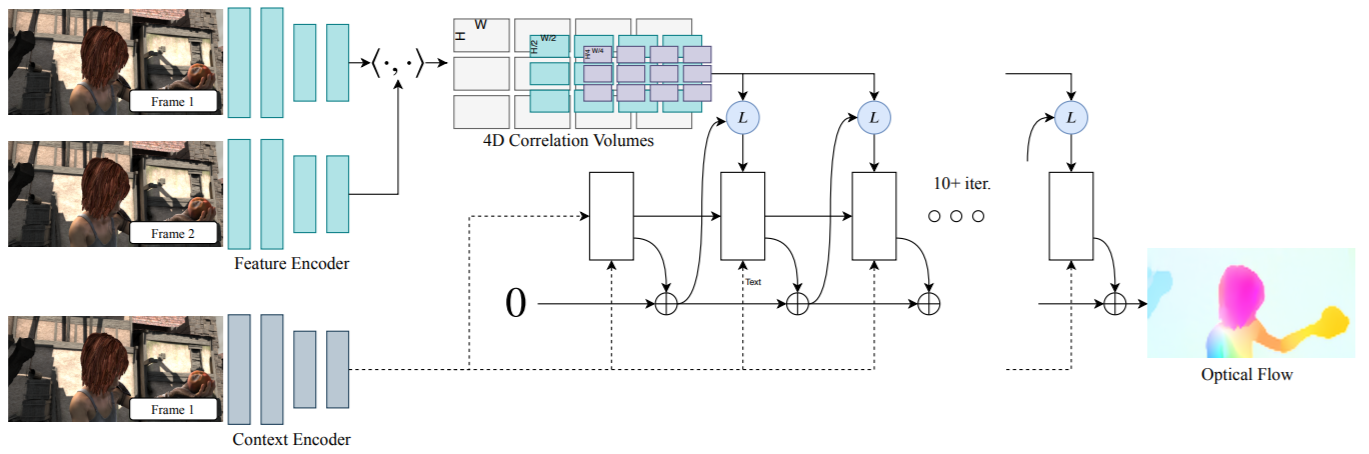
일단 두 개의 이미지(t frame, t+1 frame)을 input으로 넣는다. 그리고 optical flow를 계산하여 n 번의 iteration으로 반복한다. 이 방법이 본 논문의 저자가 말하는 가장 큰 contribution이다.
본 네트워크의 구조는 3가지고 구분할 수 있다. 앞 단은 Feature Extractor, 그리고 4D corrleation Volumes 부분을 Corrleation Volume 부분, 마지막으로 나머지 아키텍쳐 부분은 GRU structure 이다.
### Feature Extraction

feature extractor 부분은 위 그림처럼 구성된다. 간단한 CNN 구조로 이뤄진다.
이러한 Feature extractor는 두 부분으로 나눠지는데 Fnet과 Cnet이다. Feature encoder 부분과 context encoder 부분으로 나눠지는데 fnet은 전체적인 아키텍쳐에서 하늘색 부분으로 된 부분이다. Fnet은 Motion을 위한 Feature를 추출하는 부분이다. 이는 Motion이기 때문에 Frame1과 Frame2 모두에서 추출한다.
그리고 Cnet은 Context 를 추출하는 부분인데 이 context는 이미지에서 어떤 부분이 얼굴이고 어떤 부분이 손이고 이런 것을 알려주는 것이다. 이런 context를 추출하는 것은 frame1에서만 추출을 한다.
### Corrleation Layer(Before Iteration)
본 논문의 corrleation layer는 그 전과 다르게 4d corrleation layer이다. 이 부분은 iteration을 하기 전에 추출된다.

corrleation layer를 처음에 계산하는 방법은 기존의 방식과 동일하다. 일단 위 식에서 \(g_{$theta} \)는 Feature extraction 결과이다. 그리고 4차원은 H x W x H x W 의 크기가 된다. 앞에 H x W는 Image 1에 대한 크기이고 뒤에 H x W는 Image 2에 대한 크기이다.
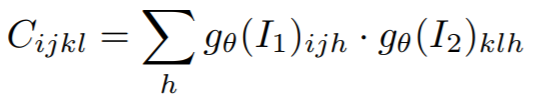
위 식을 이해하기 위해 아래의 직육면체 feature map을 이용하여 설명하겠다.

위 그림처럼 H x W x D 의 feature map이 형성되고 여기서 D는 256이다.
식 (2)의 ij는 feature map 1에 대한 위치이고, kl은 feature map2 에 대한 위치이다. 따라서 4차원 tensor (i,j,k,l)에 대하여 D = feature map의 깊이를 저장하고 이를 내적한다. 그리고 그 값을 \(C_{ijkl}\)로 저장한다.
따라서 이를 그림으로 나타내면 다음과 같다.

부연 설명을 하자면 \(H_{1}\) x \(W_{1}\) 의 크기 내에서 \(H_{2}\) x \(W_{2}\) 의 tensor가 존재하는 것이다. 이러한 구조로 구성된 것을 Corrleation volume이라고 한다.
그리고 이렇게 계산한 Corrleation volume을 Corrleation Pyramid 형식으로 만든다. 이를 식으로 표현하면 다음과 같다.
$$C^{k} : [H \times W \times\frac{H}{2^{k}} \times\frac{W}{2^{k}} ]$$
이는 위에서 구하였던 \(H_{1}\) x \(W_{1}\)의 corrleation volume을 bilinear downsampling을 한다. 이 때 위 식에서 보는 것 처럼 안에 \(H_{2}\) x \(W_{2}\) 크기만 downsampling을 진행한다. 따라서 \(H_{1}\) x \(W_{1}\)의 크기를 유지하되 내부의 사각형 크기만 줄이는 것이다.
따라서 이러한 방법으로 \(C_{1}\) 부터 \(C_{k}\) 까지 모두 구할 수 있게 된다.
### Corrleation Layer(In Iteration)
Corrlelation Layer를 구하는 과정은 Iteration 전, Iteration 중간으로 나눠져 있는데, 본 논문의 저자는 Corrleation layer는 한 번 구하고 반복 과정에는 더 간단한 방법으로 계산하기 때문에 연산 속도가 많이 느려지지 않는 다는 것이다. 즉, 앞서 언급한 연산은 단 한 번만 이뤄지고 지금부터 소개하는 연산은 iteration 수만큼 n번 이뤄지는 것이다.
이 단계에선 Corrleation Lookup 연산이 이뤄진다. 이는 4차원의 cost volume을 3차원의 corrleation feature로 변환하는 연산이다. 이는 딥러닝 연산에서 3d tensor로 만들어줘야지 연산이 되기 때문에 단순히 차원을 변환하는 과정이라고 생각해도 된다.

위 그림에서 current opitcal flow를 보자. 여기서 말하는 currnet optical flow는 아키텍쳐에서 optical flow를 계산할 때 iteration 중간 n 번째의 optical flow를 말한다. 다시 말하면 optical flow가 초기엔 \(F_{0} \)으로 초기화 되어있는 상태에서 optical flow 계산을 반복할 수록 \(F_{1} \), \(F_{2} \), \(F_{n} \) 으로 계산되게 된다. 따라서 이 중간 과정에 있는 \(F_{n}\) 을 말하는 것이다.
currnet optical flow를 자세히 보자면 화살표의 시작위치와 끝 위치를 봐보자. image 하나에서 여러개의 그리드로 나눠져 있는 것 중에 하나의 그리드만 살펴보자.
이 그리드에서 화살표의 시작위치는 첫번째 이미지의 해당 좌표를 나타내는 거고, 화살표의 끝 위치는 두번째 이미지의 해당 좌표를 나타내는 것이다. 즉, 첫번째 이미지에서 해당 좌표가 두번째 이미지의 화살표 끝점으로 옮겨진 것을 볼 수 있다.
이러한 current optical flow를 cost volume 형태로 나타내면 다음 그림과 같다.

current optical flow에서 Target 위치를 파란색 직사각형으로 나타내었다. 정확히는 한 포인트(Target point)를 주변으로 \(2r+1\) 씩 감싸고 그 사각형을 정의한 것이다.
이 사각형은 계산된 Corrleation 값이 된다. 따라서 만약에 \(I_{1}\)의 위치가 (i,j) 라고 하면 3차원 직육면체 에서 i,j 위치에 채널 깊이를 직사각형의 크기 만큼 즉, \( (2r+1)^{2} \) 의 채널이 생기게 된다.
따라서 corrleation feature map의 크기는 \( H \times W \times (2r+1)^{2} \)이 된다.
## GRU Structure(In iteration)
다음으로 GRU structure에 대해 알아보겠다. GRU는 대표적인 RNN 구조이다.
밑에 식에서 \( h_{t} \) 는 GRU의 hidden unit 이고 \( x_{t} \)는 앞서 구한 flow와 correlation feature, context feature 들을 모두 concat 한 것이다.

따라서 저 두 변수를 통해서 GRU 를 거치게 되고 최종적인 \( h_{t} \)를 얻을 수 있게 된다. 그리고 이 \( h_{t} \)를 convolution 연산 두번을 거쳐서 최종적인 \( \Delta F_{t} \) 을 얻게 된다.

따라서 최종식은 다음과 같이 쓸 수 있다.
$$ f_{k+1} = f_{k} + \Delta f_{k} $$
\(f_{k}\)는 현재 flow를 말하고 \( \Delta f_{k} \) 는 변화량을 말한다. 따라서 이 둘을 더하여 다음 flow \( f_{k+1} \)을 구하면서 이를 반복하고 최적의 flow \(F^{*}\) 를 얻게 된다.
## Training & Inference
loss function은 Ground Truth 값과의 L1 Loss 값으로 한다. 대신 마지막 flow와 gt와 비교하는 것이 아니라 반복을 하면서 얻을 수 있는 flow 값들을 모두 gt와 비교를 한다. 따라서 식은 다음과 같이 이뤄진다.

L1 loss에서 가중치를 곱해지게 되는데 본 논문에선 \( \gamma = 0.8\) 로 설정하였다. 따라서 반복이 진행되서 끝 부분에 더 큰 가중치를 곱해줘서 훈련을 시키게 하는 것이다.
그리고 inference는 기존의 구조와 동일하게 iteration을 통해서 inference를 하게 되고 initalization은 \( f_{t}(x) = 0\)으로 한다.
본 논문의 저자는 warm start를 제안한다. 본 논문의 저자는 이전 flow를 활용하기 위해 forward projection 방법을 이용하였다. 식은 다음과 같다.
$$ f_{t}(x + f_{t-1}(x)) = f_{t-1}(x) $$
이 식을 설명하자면 기존(\(f_{t-1}\) )에 있는 optical flow들의 벡터를 미리 이동을 하여 \(f_{t}\)에 대한 가이드를 해줄 수 있게 하는 것이다. 따라서 이러한 값으로 initalization에 활용한다.
그리고 inference할 때 iteration의 수는 32로 설정하였다.
## Results


매우 성능이 뛰어나서 엄청난 비약적인 발전을 하였다.

optical flow의 연산 속도 측면 같은 경우에서도 꽤 빠른 편에 속한다.
## Conclusion
성능적인 면에서 엄청난 비약적인 발전을 보여줬다.
optical flow와 같이 ground truth 없이도 input 을 통해 어느 정도의 평가가 가능한 분야에서 여러 번의 iteration을 통한 inference를 한다는 점은 매우 훌륭하다.




댓글