cs231n - Backpropogation and NN part1

## Backpropogation

Backpropogation = 역전파를 이해하기 위해 간단한 그림으로 설명을 시작한다.

역전파를 보기 전에 먼저 순전파(feedforward)부터 보자.

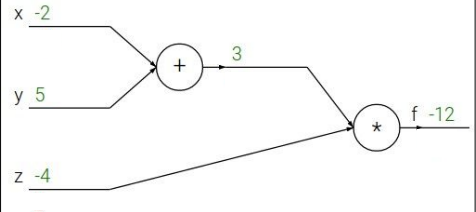
위 그래프는 $ f(x,y,z) = (x+y)z $를 그림으로 나타낸 것이다. 그리고 x = -2, y=5, z=4를 임의로 대입한다.

위 그래프처럼 +를 먼저 계산하고 그 다음에 z 값을 곱하는 순서대로 해서 최종 답 -12를 도출한다.

여기서 + 과정을 매개변수 q 라고 하자. 그러면 식은 $ q = x+y, f=qz $가 된다.

이러한 식이 도출됐을 때 간단하게 미분을 해주면 다음과 같이 된다.

$$ \frac{\partial q}{\partial x} = 1, \frac{\partial q}{\partial y} = 1 $$

$$ \frac{\partial f}{\partial q} = z, \frac{\partial f}{\partial z} = q $$

하지만 우리가 원하는 것은 input에 대해 마지막의 결과값이 어떻게 달라지는 지의 영향을 원한다.

즉, $ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} $를 원한다.

이를 위해 backward pass를 해야한다.

이를 하나씩 풀어나가자.

처음의 값 즉 $ \frac{\partial f}{\partial f} $는 1이 된다.

그리고 위에서 구한 $ \frac{\partial f}{\partial z} $는 q가 되고 이는 3 이라는 값이 된다. 이는, input z 값이 최종 f에 대해 3배 만큼의 영향력을 주고 있다는 뜻이다. z가 h 만큼 증가할 때, f는 3h 만큼 증가한단 것이다.

그리고 다음 값을 구하기 위해 f 에 대한 q의 미분을 해보자. 그럼 이것도 위에서 구하였듯이 $ \frac{\partial f}{\partial q} = z $ 가 되고 이 값은 -4 가 된다.

그러면 $ \frac{\partial f}{\partial y} $는 어떻게 구할까? 이를 구하기 위해선 Chain Rule을 이용해야한다.

즉, $ \frac{\partial f}{\partial y} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial y} $로 계산할 수 있다.

이를 숫자를 대입해서 풀어쓰면 z*1 이 되고 이는 -4가 된다. 이는 y가 h 만큼 증가할 때, f는 -4h 만큼 증가한단 것이다.

위와 같은 원리로 $ \frac{\partial f}{\partial x} $도 동일하게 계산할 수 있으며 -4가 된다.

여기서 $ \frac{\partial f}{\partial q} $는 global gradient 라고 하고, $ \frac{\partial q}{\partial y} $는 local gradient 라고 한다.

Local Gradient는 feedforward 계산 시 구할 수 있고, Global Gradient는 backward 시 구할 수 있게 된다.

이번엔 좀 더 복잡한 예시를 들어보자.

위 그래프는 sigmoid function을 통과하는 $ f(w,x) $를 그래프로 나타낸 것이다. 따라서 우리가 결국 계산해야할 것은 input에 대한 loss의 영향력을 구하는 것이다.

이를 미분을 통해서 쭉 계산을 해보자.

결과는 다음과 같이 나온다.

위 그림에서 sigmoid gate라고 표시 되어 있는 곳이 있다. 이러한 sigmoid 는 미분을 할 때 특이하게 값이 나온다. 그리고 매우 간단하다.

$$ \frac{d\sigma (x) }{dx} = \frac{e^{-x} }{ (1+e^{-x})^{2} } = (1-\sigma (x))(\sigma (x))$$

위 식처럼 전개된다. 따라서 파란색 박스 왼쪽에 있는 0.2라는 숫자는 (0.73) * (1-0.73) 으로 나타낼 수 있는 것이다.

이러한 feedforwad propogation과 backpropogation을 pseudo code로 나타내보자.

class MultiplyGate(object):
      def forward(x,y):
        z = x*y
        self.x = x
        self.y = y
        return z
      def backward(dz):
        dx = self.y * dz
        dy = self.x * dz
        return [dx,dy]

이 코드는 x*y = z 를 코드로 나타낸 것이다. z를 x로 미분한 값, z를 y로 미분한 값을 통해서 backward가 완성되는 것이다.

## Gradient for Vectorized code

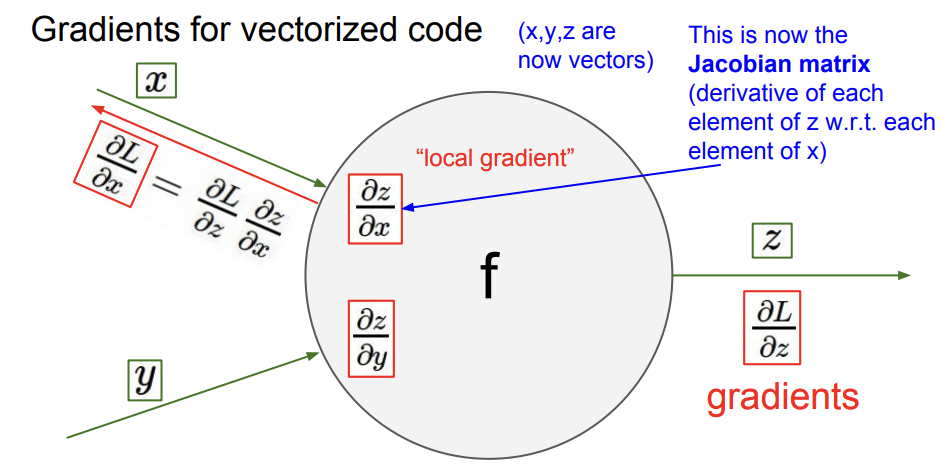
실제 데이터는 matrix 형태로 계산되기 때문에 vector 형태의 계산을 해야한다. 이 때, local gradient는 미분값으로 이뤄진 행렬 jacobian matrix가 된다.

만약에 4096x1 size 의 input vector로 들어온다하면 output vector도 동일한 사이즈로 나오게 된다. 그리고 이 때 중간과정인 jacobian matrix는 4096x4096 shape이 되게 된다.

이런 shape를 잘 이해하여 code를 작성해야한다.

## Neural Network(NN)

그 전까지는 Linear Score function으로 $ f= Wx $를 사용하였지만 이젠 2개 이상의 Layer를 통과하는 Neural Network에 대해서 알아본다. $f = W_{2} max(0, W_{1}x$를 사용한다.

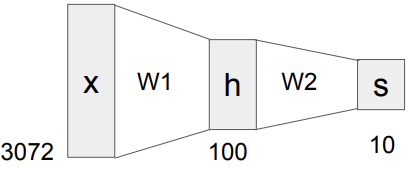
예를 들어 CIFAR10의 데이터셋을 input 값으로 들어간다 하자. 위 그림처럼 w1 이라는 weight 값 matrix를 통과한 후 중간의 h라는 hidden layer를 통과한다. 그리고 여기서 hidden layer를 통과한 값들에 또 w2라는 weight 값을 통과시켜서 s라는 output layer로 나오게 된다. 이는 10개의 클래스를 분류할 수 있게 한다.

여기서 hidden layer 100개에서 hidden node 각각이 하나의 feature를 담당한다고 생각하면 된다. 예를 들어 hidden node 하나는 앞쪽을 보고 있는 빨간색 자동차를 담당하고 있다라고 생각하면 된다.

본 강의에선 2 layer NN에 training 방법을 소개한다.

import numpy as np
from numpy.random import randn

N,D_in,H,D_out = 64,1000,100,10
x,y = randn(N,D_in),randn(N,D_out)
w1,w2 = randn(D_in,H), randn(H,D_out)

for t in range(2000):
	h = 1/1(np.exp(-x.dot(w1)))
    y_pred = h.dot(w2)
    loss = np.square(y_pred - y).sum()
    print(t,loss)
    
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h.T.dot(grad_y_pred)
    grad_h = grad_y_pred.dot(w2.T)
    grad_w1 = x.T.dot(grad_h * h * (1-h))
    
    w1 -= 1e-4 * grad_w1
    w2 -= 1e-4 * grad_w2

## Activation Function 종류