## Centrality
graph에서 중앙 역할을 하는 node(= 중요한 역할을 함)
그럼 중앙 역할의 의미가 무엇일까? 이는 중앙 역할의 정의에 따라 달라진다.
이러한 Centrality의 종류는 4가지가 있다.
- Degree Centrality : 많은 degree를 가진 노드가 중요할 것
- Closeness centrality : 관계 중요도(weight) 기반
- Betweennewss Centrality : Dense와 Dense를 연결해주는 subnetwork 노드
- Eigenvector Centrality : 큰 네트워트를 연결
## Degree Centrality
많은 degree를 가진 노드가 가장 중요할 것이다라는 생각에서 파생된 개념
Degree Centrality는 다음과 같이 계산된다
$$ C_{D}(v_i ) = \frac{1}{N-1}d_{i} $$
여기서 N = node의 수 이고 \( d_{i} \)는 i 번째 노드의 degree 수이다

위와 같은 예시에서 두번쨰 그래프 가운데 노드에 대해 계산해보자
해당 그래프의 총 노드의 개수 = 7 d_i = 2 -> 2/(7-1) = 1/3
## Closeness Centrality
다른 노드들과 가장 짧은 거리를 가진 node가 가장 중요한 역할을 한다는 관점에서의 centrality다
$$ C_{C}(v_i ) = \frac{N-1}{\Sigma_{v_j \in G} d(v_i ,v_j )} $$
여기서 분모를 보면 분모는 모든 노드와 노드 거리의 합을 의미한다. 따라서 이는 Noramlization을 한 거리 기반 centrality이다.

여기서 거리는 모두 한 edge의 길이 = 1로 보고 계산하고 다른 노드로 가기 위한 최소 거리를 거리라고 정의한다.
아까와 같은 그래프를 계산해보면 (7-1)/(1+2+2+1+2+2) = 3/5 가 나온다.
## Betweenness Centrality
community의 bridge 역할이 centrality 라는 생각에서 파생된 개념이다. 즉, 이와 같은 역할은 control of information의 역할을 한다는 주장이다. (예를 들어 브로커 역할)
식은 다음과 같다
$$ C_B (v_i) = \frac{\Sigma_{j<k} \frac{g_{jk}(v_i) }{ g_{jk} }}{\frac{(N-1)(N-2)}{2}} $$
여기서 분자는 자신을 거쳐서 연결이 되어있는 지를 판단하고 분모는 자신으로부터 도달 가능한 모든 pari의 수를 말한다. 즉 여기서 분모는 \({}_{n-1} C_2\) 를 의미한다.
따라서 Betweenness Centrality는 연결되기 위해서 반드시 나를 거쳐가야 하는지를 판단하는 지표이다.

일단 위 그래프에서 (6*5) / 2 이므로 분모는 15가 된다.
네트워크의 모든 노드 쌍 간의 shortest path가 해당 노드를 지나는지를 파악해야되기 때문에 임의로 노드에 번호를 붙여보자
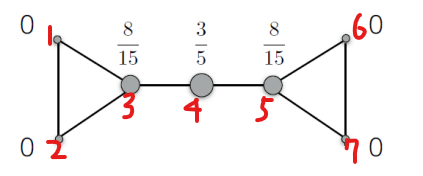
1번 노드부터 시작하여 4번 노드를 거치는 모든 경우의 수를 구해보자
(1-5),(1-6),(1-7)(2-5),(2-6),(2-7),(3-5),(3-6),(3-7)로 총 9가지의 경우가 나온다. 따라서 분자는 9이다.
결론은 9/15가 나오게 된다.
## Eigenvector Centrality
중요한 사람들을 추출하는 metric. eigen vector 추출 방식과 동일함
중요한 역할을 하는 노드들과 연결되어 있는 것들이 eigenvector가 더 높다는 방식을 이용
## Comparision
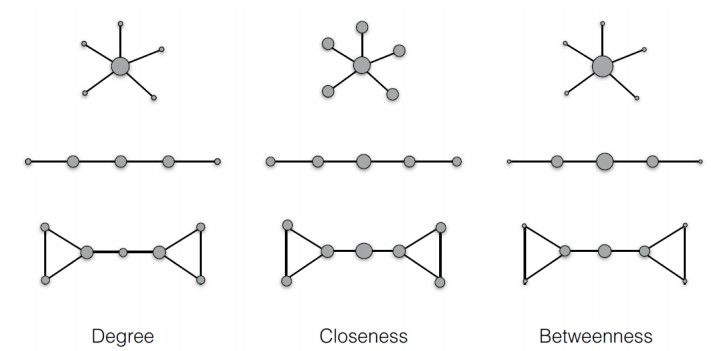
## Network centralization
- High centralization을 갖고 있으면 하나의 노드가 중심으로 그래프가 구성된다는 것
- Low centralization을 갖고 있으면 일대일 trade가 많고 분산이 크다는 것
## Pretige
Directed graph의 centrality
'Graph Mining' 카테고리의 다른 글
| Newman Method (0) | 2021.12.08 |
|---|---|
| Communities (0) | 2021.12.08 |
| Structure Role in Network (0) | 2021.12.07 |
| Extract Subgraph Enumeration(ESU) (0) | 2021.12.07 |
| Graphlets (0) | 2021.12.07 |




댓글