## Newman Method
Newman Method는 Edge Betweenness를 이용한 communities detection method 이다.
여기서 edge betweenness는 betweenness centrality(2021.12.08 - [Graph Mining] - Centrality)의 edge 버전이라고 생각하면 된다.
즉, 두 community를 연결해주는 weak edge가 betweenness centrality가 가장 높다.

Newman Method는 undirected, unweighted network에서만 동작한다.
이 method의 진행과정은 다음과 같다.
- 모든 edge에 대해서 edge betweenness를 계산
- 가장 값이 높은 것을 제거
- connected component의 개수를 셈
- 다시 그 상태에서 edge betweenness 계산 후 최댓값 edge를 제거
- edge가 다 사라질 때 까지 1~4 반복
- 나온 값 중에 edge betweenness가 높은 값을 선택
그림으로 보면 다음과 같다.

먼저 edge betweenness가 가장 놓은 edge가 제거 된다. 그러면 두개의 dense 한 community로 나눠지게 된다. 다음으로 또 edge betweenness가 가장 놓은 edge가 제거되고, 커뮤니티가 나눠지게 된다. 이를 반복하였을 때 모든 node만 남게 된다. 마지막으로 이 노드들을 hierarchical network deomposition을 하여 clustering 해준다
## Edge Betweenness
Edge Betweenness의 작동 과정은 다음과 같다.

왼쪽과 같은 graph가 있을 때 처음엔 A를 중심으로 BFS를 생성한다.

두번째로 이러한 BFS에서 A노드로부터 다른 노드로 이동하기 위한 shortest path를 구한다.
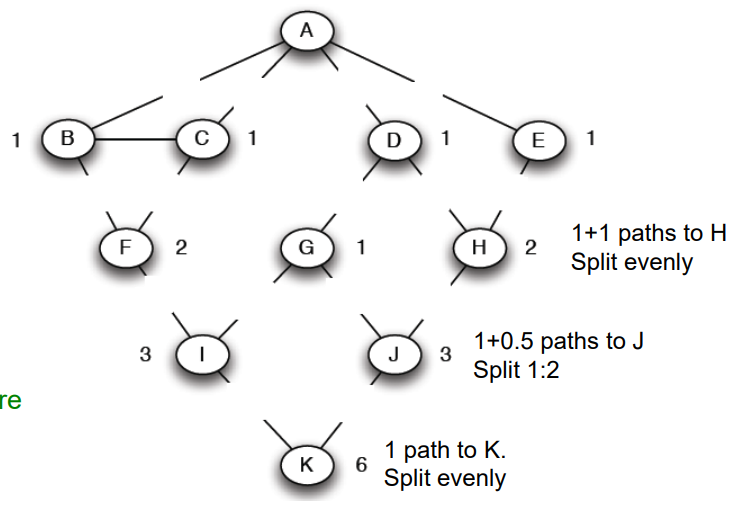
세번째로 각 노드에서 edge betweenness를 계산한다.
이 때, 자신의 node flow는 1+\( \Sigma child node flow \) 이다.
정확한 이해를 위해 예시를 들어 설명하겠다.
K 노드에서 edge betweenness를 구하는 과정을 설명한다. K node에선 자식노드의 node flow가 없으니 1+0으로 1이 나온다. 그리고 여기서 두갈래로 뻗어 있으니 parents의 비율을 보고 판단한다. 여기서 parents node는 3,3 으로 1:1 비율이기 때문에 K-I , K-J 로 가는 edge의 edge betweenness 는 각각 1/2, 1/2 다.
다음으로 J에 대해서 계산해보겠다.
J의 child node flow는 1/2로 J node의 node flow는 1+1/2 = 3/2 이다. 여기서 parents node인 G와 H를 보자. 이 노드의 비율은 1:2 이다. 따라서 G 노드로 뻗어나가는 edge betweenness는 3/2 X 1/3 = 1/2 , H 노드로 뻗어나가는 edge betweenness는 3/2 X 2/3 = 1 이다. 따라서 이러한 결과를 보면 다음과 같은 graph가 형성된다.

그리고 이 과정을 root노드를 A~K까지 반복한다. 그러면 edge betweenness가 모두 더해지게 되고 edge betweenness가 큰 것을 기준으로 정렬한다.

그리고 이 값을 기반으로 잘라서 clustering 하는 것이 Newman Method 이다
## Result
앞서 설명한 과정을 반복하다가 보면 다음과 같은 그래프의 형태를 따르게 된다.
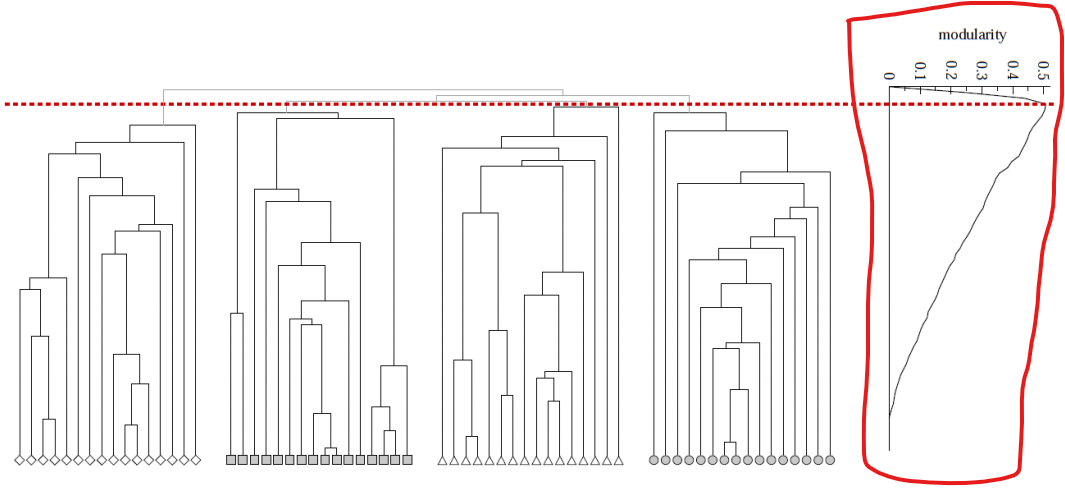
옆에 네모친 modularity plot을 한 번 봐 보자
일정 수준이 될때까지 즉, modularity가 가장 커질 때가 최적의 modularity를 가지는 것이고 이 때를 기점으로 community detection을 한다.
그러면 왜 저런 모양의 plot을 띄고 있을까?
※ 중요
- modularity가 급격하게 증가하는 이유 : week한 edge들이 제거 되었기 때문이다. week한 edge들은 edge betweenness 값이 높기 때문에 이러한 edge들이 먼저 제거 되면서 modularity는 상승한다.
- modularity가 감소하는 이유 : 최대 modularity 이후에 많은 node i - node j의 조합의 수가 감소하기 때문이다. 이는 즉, modularity 식에서 \( A_{ij} \)= 0이 많아진다는 뜻이다. 따라서 이는 modularity가 감소하는 요인이 된다.
'Graph Mining' 카테고리의 다른 글
| Lovain Algorithm (0) | 2021.12.08 |
|---|---|
| Communities (0) | 2021.12.08 |
| Centrality (0) | 2021.12.08 |
| Structure Role in Network (0) | 2021.12.07 |
| Extract Subgraph Enumeration(ESU) (0) | 2021.12.07 |




댓글