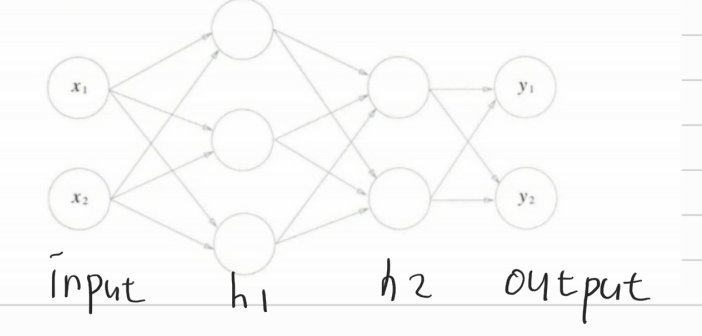
3층 신경망 구현하기
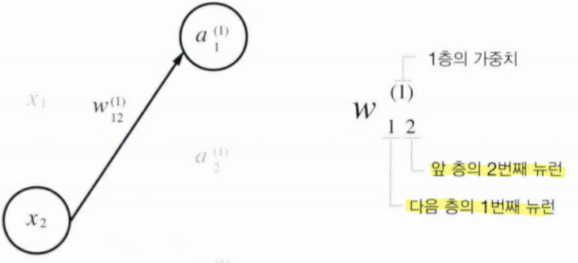
- 표기법
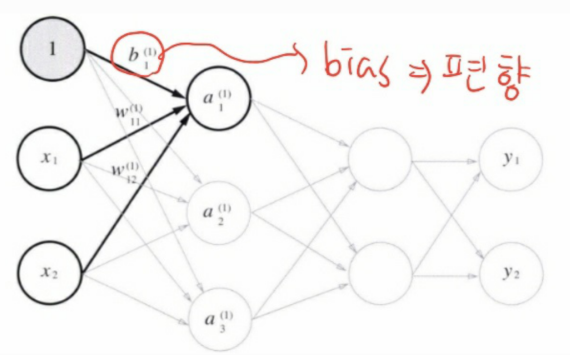
bias(편향) 값을 추가로 1층 신호의 a_1에 전달한다.
따라서 다음과 같은 식이 도출된다.
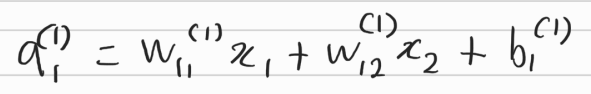
각각의 input값과 그에 대응하는 가중치가 전달되고 1번째 편향을 더해준다.
이를 행렬로 표현하면
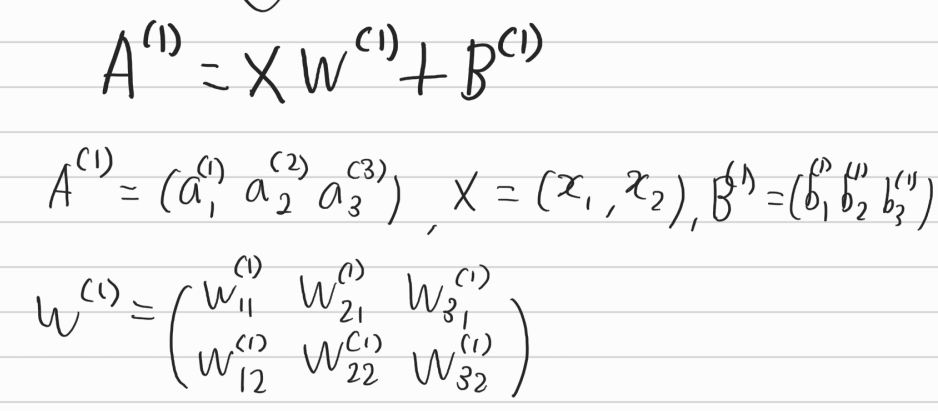
위와 같이 표현이 된다.
그리고 1층 layer에선 입력값과 가중치 그리고 편향을 전달받고 1층 내에선 앞서 언급한 활성화 함수(activation function)을 적용시킨다. 여기선 sigmoid 함수를 적용시킨다.
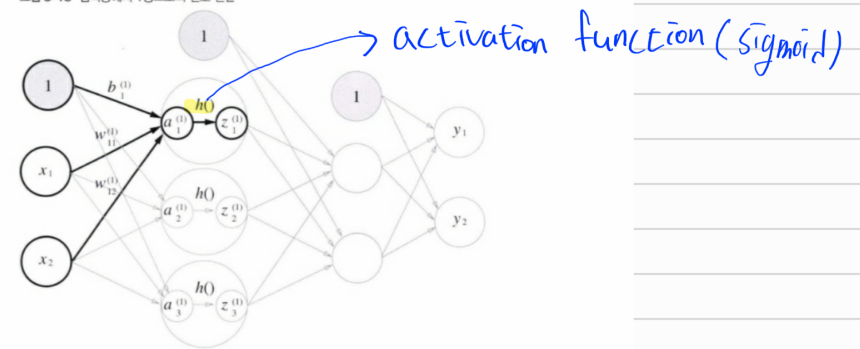
활성화 함수는 h() 라고 표현하며 h(a1)으로 1층 layer의 첫번째 값이 sigmoid 활성화 함수를 적용 받았음을 표현한 것이다.
다음 레이어와 output 레이어까지도 같은 원리가 작동한다.
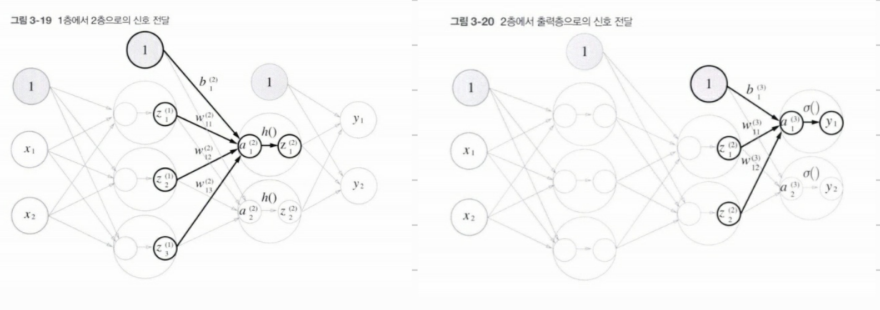
지금까지의 과정을 코드로 표현해보겠다.
# Input -> 1 layer
X = np.array([1.0,0.5]) # Input
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]]) # 가중치
B1 = np.array([0.1,0.2,0.3]) # bias
print(X.shape)
print(W1.shape)
print(B1.shape)
A1 = np.dot(X,W1)+B1
print(A1)
Z1 = sigmoid(A1)
print(Z1)
'''
(2,)
(2, 3)
(3,)
[0.3 0.7 1.1]
[0.57444252 0.66818777 0.75026011]
'''각각의 shape을 통해 행렬 연산이 가능함을 보여준다. 그리고 마지막에 Z1은 A1에서 계산된 값을 활성화 함수 sigmoid 함수가 적용된 것이다.
# 1layer -> 2layer
W2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2 = np.array([0.1,0.2])
print(Z1.shape)
print(W2.shape)
print(B2.shape)
A2 = np.dot(Z1,W2) + B2
Z2 = sigmoid(A2)
print(A2)
print(Z2)
'''
(3,)
(3, 2)
(2,)
[0.51615984 1.21402696]
[0.62624937 0.7710107 ]
'''# 2layer -> output
def identitiy_function(x):
return x
W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])
A3 = np.dot(Z2,W3)+B3
Y = identitiy_function(A3)
print(Y)
'''
[0.31682708 0.69627909]
'''2층 layer에서 output으로 전달될 때 마지막에 identity_function을 사용하였는데 이는 쉽게 말하면 등호 표시이다.
통일성을 위해 굳이 identity_function을 만들어서 자기 자신의 값을 return 해주는 함수를 만든것이다.
위와 같은 반복과정을 함수화 해서 정리해보자
def init_network(): # 가중치와 편향 초기화
network = {}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2'] = np.array([0.1,0.2])
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def forward(network,x) : # 순방향
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y = identitiy_function(a3)
return y
network = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
print(y)
'''
[0.31682708 0.69627909]
'''init_network()를 통해 가중치와 편향을 저장한 후 forward를 통해 연산을 진행함을 알 수 있다. 이러한 방식은 순방향이라고 한다.
## 출력층 설계하기
위 코드에서 굳이..?라고 생각한 사람이 있을 것이다. 바로 identity function이다. 굳이 저 과정을 해줘야하나라는 의구심이 들텐데 이를 설명하겠다.
신경망에는 두가지를 구현할 수 있다. 바로 회귀(regression)와 분류(classification)이다.
일반적으로 회귀에선 출력층에 identity function(항등 함수)를 활성화 함수로 적용 시킨다. 회귀 자체는 있는 그대로의 값을 반환해야되기 때문에 항등 함수로 구현한다.
그렇다면 분류에선 어떠한가? 분류에선 소수점이라는 float type이 아닌 int, category 형식이 나와야한다. 남자인지 여자인지 분류 하려는데 0.7 이라는 것이 나오면 이는 남자인지 여자인지 모르는 상황이기 때문에 다른 형식의 변환이 필요하다. 이를 가능하게 하는 것은 softmax function이다.
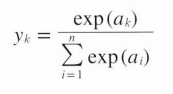
왼쪽의 식에서 n은 출력 뉴런의 수(반환한 class 수), a_k 는 입력 신호를 뜻한다.
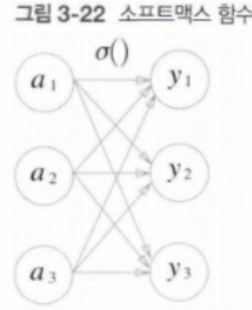
왼쪽의 그림과 위의 softmax 식에서도 알 수 있듯이 출력 값은 모든 입력신호에 영향을 받음을 알 수 있다.
이를 코드로 나타내보자
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
예시의 input 값을 넣어서 적용해보자.
a = np.array([0.3,2.9,4.0])
exp_a = np.exp(a)
print(exp_a) # [ 1.34985881 18.17414537 54.59815003]
sum_exp_a = np.sum(exp_a)
print(sum_exp_a) # 74.1221542101633
y = exp_a/sum_exp_a
print(y) # [0.01821127 0.24519181 0.73659691]
input의 개수만큼 y가 반환된다.
softmax 함수를 구현시 주의할 점이 한가지 있다. 바로 overflow 문제점이 발생할 수 있다는 것이다.
softmax함수는 지수 함수로 구현되어 있기 때문에 아주 큰 값을 input 값으로 집어 넣는다면 inf로 수렴한다.
이러한 문제점을 개선한 식은 다음과 같다.
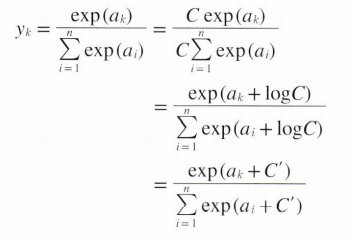
C라는 임의의 상수를 각 분자 분모에 곱해준 후 이를 exp 안에 집어 넣어 log를 취한다. 그런 후 logC를 C'라는 새로운 기호로 만든다.
여기서 C' 에 어떠한 값을 넣어도 값에 변화가 없지만 overflow를 막을 목적으로는 input 값의 maximum을 C'에 넣어준다.
a = np.array([1010,1000,990])
np.exp(a)/np.sum(np.exp(a)) # 너무 크면 계산 불가
# array([nan, nan, nan])
c = np.max(a) # input의 최댓값
a-c # array([ 0, -10, -20])
np.exp(a-c) / np.sum(np.exp(a-c)) # array([9.99954600e-01, 4.53978686e-05, 2.06106005e-09])
c를 하나 빼줌으로써 계산이 가능하게 된다.
개선한 softmax함수를 알아보자
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c) # prevent overflow
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
softmax함수에는 특징이 하나 있다. 눈치 빠른 사람이라면 이미 눈치 챘을 수도 있겠지만 output의 값을 모두 더하면 1이 된단 것이다. 이는 즉 각 클래스일 확률이라고 정의할 수 있다.
그리고 softmax함수는 단조 증가 함수(ex. y=x,y=2x) 이기 때문에 각 output원소의 크기가 변화하지 않는다.
따라서 input 값에서 가장 큰 원소가 2번째에 있다면 출력값에서도 가장 큰 원소는 2번째에 있는 것이다.
※ softmax는 train 할 때만 적용시킨다! 지수 함수의 연산을 줄이기 위해서 train에선 출력층에 softmax함수를 적용시키지만 test과정에선 softmax 함수는 생략한다.
'밑바닥 딥러닝' 카테고리의 다른 글
| Chapter5 - Backpropogation (0) | 2021.07.03 |
|---|---|
| Chapter4 - Training Neural Network(1) (0) | 2021.02.02 |
| Chapter3 - Neural Network(3) (0) | 2021.01.10 |
| Chapter3 - Neural Network(1) (0) | 2021.01.10 |
| Chapter2 - Perceptron (0) | 2020.12.28 |




댓글