2021/01/10 - [밑바닥 딥러닝] - Chapter3 - Neural Network(1)
Chapter3 - Neural Network(1)
신경망 예시 맨 왼쪽 층을 입력층, 가운데 층을 은닉층, 맨 오른쪽 층을 출력층 가중치를 갖는 층(화살표가 있는) 2개 이므로 ‘2층 신경망’ 활성화 함수 활성화 함수(Activation Function) : 입력 신호
bigdata-analyst.tistory.com
2021/01/10 - [밑바닥 딥러닝] - Chapter3 - Neural Network(2)
Chapter3 - Neural Network(2)
3층 신경망 구현하기 - 표기법 bias(편향) 값을 추가로 1층 신호의 a_1에 전달한다. 따라서 다음과 같은 식이 도출된다. 각각의 input값과 그에 대응하는 가중치가 전달되고 1번째 편향을 더해준다.
bigdata-analyst.tistory.com
그 전 글에서 이론을 공부했으니 이제 실제 데이터셋에 적용하여보자
가장 대표적인 데이터셋인 MNIST를 불러올 것이다.
일단 github.com/WegraLee/deep-learning-from-scratch
WegraLee/deep-learning-from-scratch
『밑바닥부터 시작하는 딥러닝』(한빛미디어, 2017). Contribute to WegraLee/deep-learning-from-scratch development by creating an account on GitHub.
github.com
위 저자 깃허브에 접속하여 load_mnist.py 를 다운 받는다. 그리고 작업 디렉토리에 그 파이썬 파일을 위치시킨다.
나는 mnist.py라 이름을 바꾸어 저장하였다. 그리고 다음과 같은 코드를 작성한다.
sys.path.append(os.pardir)
from mnist import load_mnist
(x_train,t_train),(x_test,t_test) = load_mnist(flatten=True,normalize=False)
print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)
'''
(60000, 784)
(60000,)
(10000, 784)
(10000,)
'''
다운 받은 pickle 파일이 정상적으로 작동하는지 한 번 시각화를 한다.
from PIL import Image
def img_show(img):
pil_img = Image.fromarray(np.uint8(img))
pil_img.show()
img = x_train[0]
label = t_train[0]
print(label) # 5
print(img.shape) # (784,)
img = img.reshape(28,28)
print(img.shape) # (28,28)
img_show(img)

위 코드에 대해서 간략히 설명하자면 Image.fromarray 라는 함수를 통해 array 타입으로 되어 있는 image를 그림으로 인식하여 보여주는 것이다. 이 데이터를 사진으로 출력하기 위해 28x28 사이즈로 변환 시킨다.
데이터를 확인했으니 이제 신경망에 넣어 예측을 해보자
import pickle
def get_data():
(x_train,t_train),(x_test,t_test) = load_mnist(flatten=True,normalize=True,one_hot_label=False)
return x_test,t_test
def init_network():
with open("sample_weight.pkl",'rb') as f: # github에서 다운로드
network = pickle.load(f)
return network
def predict(network,x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y = softmax(a3)
return ysample_weight의 pickle 파일도 github에서 다운을 한다.
get_data()에서 적용된 옵션은 flatten은 이미지를 1차원 배열로 만들 것인지에 대한 옵션이다.(np.array.flatten())
그리고 normalize 는 0~255 까지 있는 픽셀 값을 minmax scaling 하여서 0~1 사이로 만들어주는지에 대한 옵션이고 one_hot_label은 label이 0,1,2,3... 이런 식으로 되어 있는데 이를 onehotencoding을 적용할지 말지에 대한 옵션이다.
그리고 init_network()는 이미 학습시킨 weight파일을 불러오는 것이고 predict는 그 전 포스팅에서 순방향 알고리즘을 썼을 때와 동일하게 진행된다. 활성화 함수는 sigmoid function을 쓰고 출력에선 softmax를 적용시킨다.
이에 대한 정확도를 test해보겠다.
x,t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network,x[i])
p = np.argmax(y)
if p == t[i]:
accuracy_cnt += 1
print('Accuracy: '+ str(float(accuracy_cnt)/len(x)))
# 0.9352
약 93.5퍼센트의 정확도가 나왔다. 꽤 좋은 정확도라고 할 수 있다.
## 배치처리
이번에는 batch 처리를 하여 테스트를 할 것이다.
Batch 처리란 묶음이라고 생각하면 된다. 이미지를 batch_size 만큼 묶어서 처리한다는 것이다.
배치 처리 하지 않은 신경망의 형상을 본다면
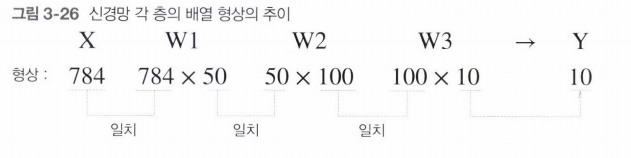
다음으로 batch_size = 100 으로 준 후의 신경망 배열의 형상이다.

100장을 한 번에 묶어 처리하는 것이다.
배치는 왜 하는 것일까? 배치를 사용하면 CPU 또는 GPU의 연산 횟수를 줄일 수 있기 때문이다. 컴퓨터는 작은 것을 여러번 계산하는 것보단 큰 배열을 한꺼번에 연산하는 것이 더 효율적이기 때문이다.
따라서 이번 모델에선 batch_size = 100으로 주고 돌려보겠다.
x,t = get_data()
network = init_network()
batch_size = 100
accuracy_cnt = 0
for i in range(0,len(x),batch_size):
x_batch = x[i:i+batch_size]
y_batch = predict(network,x_batch)
p = np.argmax(y_batch,axis=1)
accuracy_cnt += np.sum(p == t[i:i+batch_size])
print('Accuracy: '+ str(float(accuracy_cnt)/len(x)))
# Accuracy: 0.9352
정확도는 변함이 없다.
코드를 하나하나 보자면 x_batch 에서 인덱싱을 하였다. 즉 i=0일때 x[0:100], i=100일때 x[100:200] 이런 식으로 간다.
for문에 step을 batch_size 로 지정했으므로 0,100,200 이런 식으로 for문이 진행된다. 따라서 그 전의 코드보단 반복횟수가 줄어드는 것이다.
'밑바닥 딥러닝' 카테고리의 다른 글
| Chapter5 - Backpropogation (0) | 2021.07.03 |
|---|---|
| Chapter4 - Training Neural Network(1) (0) | 2021.02.02 |
| Chapter3 - Neural Network(2) (0) | 2021.01.10 |
| Chapter3 - Neural Network(1) (0) | 2021.01.10 |
| Chapter2 - Perceptron (0) | 2020.12.28 |




댓글