## 신경망 학습이란?
- 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것
- 손실함수의 결과값을 가장 작게 만드는 가중치 매개변수를 찾는 것이 학습의 목표이다.

신경망은 이미지를 있는 그대로 학습하여 이미지에 포함된 중요한 특징까지 기계가 스스로 학습 하는 것이다. 머신러닝과 다른 점은 사람이 특징점을 알고리즘을 통해 직접 찾아야하는 것이지만 신경망은 특징점조차도 자동으로 찾게 하는 것이다. 따라서 딥러닝을 end-to-end machine learning 이라고 부른다. 이는 입력에서 출력을 사람의 개입없이 얻는다는 뜻이다.
## Train set과 Test set을 분리하는 이유
- 범용 능력을 제대로 평가하기 위해 나누는 것이다.
- 범용능력이란 아직 보지 못한 데이터로도 문제를 올바르게 풀어낼 수 있는 능력을 말한다.(즉, Overfitting 방지)
## 손실함수
신경망 학습은 최적의 매개변수를 탐색하는 것이라고 앞서 언급을 하였다. 이 때 최적이라는 기준을 어떤 방식으로 세우느냐가 중요하다. 이 기준을 손실함수(Loss Function)으로 잡는다. 손실함수는 신경망 성능의 '나쁨의 정도'를 표현한다.
대표적인 손실함수로 MSE와 Cross Entropy 함수가 있다.
- MSE

def sum_squares_error(y,t):
return 0.5*np.sum((y-t)**2)MSE를 파이썬으로 나타내면 다음과 같다. MSE를 한 번 테스트해보겠다.
t = [0,0,1,0,0,0,0,0,0,0] # label=2
y = [0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0] # 2일 확률이 가장 높다
sum_squares_error(np.array(y),np.array(t))
# 0.09750000000000003t가 정답값 레이블(OneHotEncoding 형태)이고 y는 softmax를 통해 나온 결과값이다. 즉, 각 레이블이 정답일 확률을 반환한 값이다. 이 때 label 2가 가장 높다고 예측을 한 것이다. 정답값도 Label=2가 맞기 때문에 위의 MSE 손실함수 값은 0.0975로 매우 낮게 나온다.
반면에 틀리게 예측했을 때는 MSE의 값이 어떻게 나올까?
y = [0.1,0.05,0.1,0.0,0.05,0.1,0.0,0.6,0.0,0.0] # 7일 확률이 가장 높다
sum_squares_error(np.array(y),np.array(t))
# 0.59750.5975로 확연하게 높은 손실값이 반환됨을 알 수 있다.
- Cross Entropy
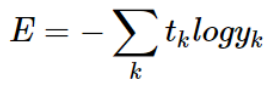

CrossEntropy를 파이썬 함수로 나타내면 다음과 같다.
def cross_entropy_error(y,t):
delta = 1e-7 # 절대 0이 되지 않도록 만듦
return -np.sum(t*np.log(y+delta))이 때 delta는 log0이면 발산하기 때문에 이를 방지하기 위해 작은 값을 더해주는 것이다.
왼쪽과 같은 그래프를 보면 0일 때 -inf 값으로 발산하는 것을 볼 수 있다.
또한, 이 그래프를 보면 정답에 해당하는 출력이 커질수록(x값이 커질수록) 값이 0(y축)에 가까워진다는 것을 알 수 있다.
Cross Entropy 함수도 테스트를 해보겠다.
t = [0,0,1,0,0,0,0,0,0,0] # label=2
y = [0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0] # 2일 확률이 가장 높다
cross_entropy_error(np.array(y),np.array(t))
# 0.510825457099338정답을 맞췄을 때 높은 MSE보단 높은 손실값이 나온다.
y = [0.1,0.05,0.1,0.0,0.05,0.1,0.0,0.6,0.0,0.0] # 7일 확률이 가장 높다
cross_entropy_error(np.array(y),np.array(t))
# 2.302584092994546이 또한 MSE보다 더 높은 손실값을 갖는다.
- 미니 배치 학습의 손실함수
지금까진 데이터 하나의 손실함수를 살펴보았다. 이를 미니배치로 하여 적용하여 보자
미니 배치의 Cross Entropy는 다음과 같다.

위 식은 모든 데이터에 대한 Cross Entropy 오차 합을 나타낸다.
이 때 N은 데이터의 개수이고 t_nk는 n번째 데이터의 k번째 값(정답값), y_nk는 n번째 데이터의 k번째 값(예측값)을 의미한다. 여기서 N(데이터의 개수)를 나누는 이유는 정규화를 통해 모든 데이터에 대한 평균 손실함수를 구할 수 있기 때문이다.
하지만 모든 데이터를 가지고 Cross Entropy를 계산하지 않는다. 왜냐하면 모든 데이터를 가지고 계산하면 시간이 너무 오래걸리기 때문이다. 이를 방지하기 위해 데이터의 일부를 추려 근사치로 이용하고 이를 미니배치(mini batch)라고 부른다.
python 코드는 다음과 같다.
def cross_entropy_error(y,t): # label = onehotencoding
if y.ndim == 1:
t = t.reshape(1,t.size)
y = y.reshape(1,y.size)
batch_size = y.shape[0]
return -np.sum(t*np.log(y+1e-7))/batch_size위는 label이 OneHotEncoding으로 되어있을 때 코드이다.
def cross_entropy_error(y,t): # label = number label
if y.ndim == 1:
t = t.reshape(1,t.size)
y = y.reshape(1,y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size),t]+1e-7))/batch_size위는 label이 숫자값으로 되어있을 때의 코드이다.
지금까지 손실함수에 대해 다뤘는데 왜 정확도를 평가지표로 사용하지 않고 손실함수로 사용하는 지에 대해 궁금증이 있을 것이다. 이 이유에 대해 설명하겠다.
- 왜 손실함수가 지표일까?
일단 '미분'의 역할에 주목해야한다. 최적의 매개변수 값을 탐색할 때 손실함수의 값을 가능한 한 작게 하는 매개변수 값을 탐색하는데 이 때 매개변수의 기울기를 계산하고 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복한다.
※손실 함수의 미분이란 가중치 매개변수의 값을 아주 조금 변화시켰을 때 손실 함수가 어떻게 변하는지의 의미
만약 미분 값이 음수이면 가중치 매개변수를 양의 방향으로 변화시켜 손실 함수의 값을 줄일 수 있고 그 반대 상황이면 반대로 움직이면 된다. 만약에 미분값이 0이 되면 어느 쪽으로 움직여도 손실 함수의 값은 줄어들지 않는다.
이와 같은 이유로 정확도가 아닌 손실 함수를 지표로 사용하는 것이다. 정확도는 대부분의 장소에서 매개변수의 미분 값이 0이 되기 때문이다.
예시를 들면 만약에 정확도가 지표였을 때라고 해보자. 100장 중에 32장을 올바르게 인식했을 때 정확도는 32%가 된다. 이 때 매개변수의 값을 아주 약간만 조정했을 때 이 정확도 지표는 변화가 있겠는가? 32에 0.001만 변해도 정확도는 32퍼센트로 유지가 된다. (정확도 = 맞은 개수/전체 개수) 따라서 정확도는 연속적인 값이 아니라 불연속적인 값이기 때문에 매개 변수를 약간 조정했을 때 변화가 눈에 띄지 않는 것이다.
반면 손실함수 일 때는 어떠한가? 손실 함수는 0.92543 이라는 수치로 나오는데 이 때 매개변수가 약간씩 변할 때도 이 값에 맞춰 0.93432와 같은 연속적인 수치로 변화하게 된다. 즉, 약간의 변화에도 민감하게 변하는 것이다.
이러한 이유로 인해 손실함수의 값을 지표로 삼는 것이다. 이는 계단함수를 활성화 함수로 사용하지 않는 이유와 동일하다.

계단 함수를 미분하였을 때는 대부분의 구간에서 0이기 때문에 값이 갱신이 안된다. 따라서 계단 함수도 위와 같은 이유로 활성화 함수로 사용하지 않는다.
'밑바닥 딥러닝' 카테고리의 다른 글
| Chapter5 - Backpropogation (0) | 2021.07.03 |
|---|---|
| Chapter3 - Neural Network(3) (0) | 2021.01.10 |
| Chapter3 - Neural Network(2) (0) | 2021.01.10 |
| Chapter3 - Neural Network(1) (0) | 2021.01.10 |
| Chapter2 - Perceptron (0) | 2020.12.28 |




댓글