## Subnetwork
그래프를 이루는 특정 노드 집합(edge)의 집합 = building block
## Subgraph
노드의 번호는 상관하지 않고 edge의 방향 구조만 상관 있음. 즉, 모양만 고려한다. 이를 non-isomorphoic 하다라고 한다.
노드가 3개 있을 때 나올 수 있는 subgraph는 다음과 같이 13개가 있다.

위 그림과 같은 13가지의 subgraph가 얼마나 있는지 세는 것이 다음에 다룰 motif 분석의 핵심이다.
그러면 이러한 subgraph의 개수를 통해 어떤 지표를 나타낼 수 있을까?
이 지표는 significance 라고 한다.
예시를 들어 significance에 대해 설명하겠다.
내가 만든 그래프에 #1 번 모양의 subgraph의 개수가 10개가 있다고 가정하자. 그리고 random graph 모델을 생성하고 #1 번의 subgraph가 3개 있다고 하자.
그러면 내가 만든 모델에서 #1 번 모양에 대한 significance가 크다고 할 수 있다.
따라서 이를 비교하여 #x 에 대해 my graph - random graph > 0 이면 positive values를 가진다 하고 otherwise 이면 negative value를 가진다.
이러한 significance 비교를 통해 어떠한 특성을 많이 가지는지 알 수 있다.
## Network motifs
motif는 앞서 살짝 언급하였듯이 노드 간의 interconnection이 얼마나 반복적으로 두드러지게 나타나는 지를 보는 것이다.
motif analysis에서 필요한 개념을 먼저 정리하면 다음과 같다.
- pattern : subgraph의 모양
- recurring : pattern이 얼마나 많이 발생하는지(overlap 허용)
- significant : Random Graph에 비해 얼마나 두드러지게 나타나는지
그럼 motif 분석을 왜 하는지 이를 통해 알아낼 수 있는 것은 무엇일까?
먼저 motif 분석을 통해 알아낼 수 있는 것은 두드러진 building block이 어떻게 구성되어 있는지 알 수 있다. 또한, 이를 통해 주어진 상황에서 어떤 반응들이 이뤄지는지 분석할 수 있다.
일례로 유젼자 같은 경우는 다음과 같은 subgraph가 많이 보인다.
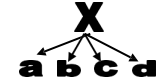
이와 같은 subgraph 모양을 보고 특정 요소가 다른 것에 영향을 미치는 broadcasting 현상이 많이 나타남을 알 수 있다.
이러한 motif 분석을 하기 위해서 앞서 언급한 significance에 대해 더 자세히 봐보자
$$ Z_{i} = (N_{i}^{real} - \bar{N}_{i}^{rand}) / std(N_{i}^{rand}) $$
\(N_{i}^{real} \) = i 번째 패턴이 real graph에서 나타난 횟수
\( \bar{N}_{i}^{rand} \) = random graph를 여러번 생성하고 그 떄의 i 번쨰에 대한 패턴이 평균적으로 몇번이 나오는지
이러한 i 번째 패턴에 대한 Z-score를 통해 Network significance profile (SP)를 계산한다.
$$ SP_{i} = Z_i / \sqrt{\Sigma_{j} Z_j} $$
이는 Z-score를 normalization 한 것으로 -1과 1 사이로 나타내고 상대적인 비교가 가능하게 차이를 파악할 수 있다.
## Configuration Model
지금까지 significance를 계산을 통해 motif 분석을 할 수 있는 방법에 대해서 알아봤다. 여기서 놓치고 있는 점이 랜덤그래프와 비교를 통해 significance를 계산하는데 이 랜덤그래프는 앞서 말한 small world의 random graph로 해결이 되지 않는다. 물론 되긴 하지만 나의 그래프와 가장 유사한 형태를 가진 random graph를 생성해야지 더 효과적인 분석이 된다.
이를 위해 configuration model에 대한 개념을 소개한다.
configuration model은 degree의 sequence를 유지하면서 내 모델과 유사한 random graph를 생성하는 방법이다. small world 와 차이점은 APL이나 clustering coefficient가 중요한 것이 아닌 내 모델과 가장 유사한 모델을 만드는 것이 핵심이기 때문에 생성 방법에 차이가 있다.
cofiguration model은 다음과 같은 방법을 통해 생성된다
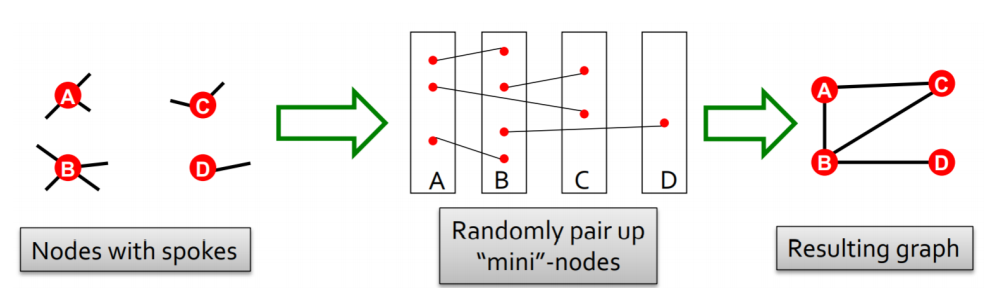
위 그림에서 노드들의 spoke가 있을 때 이러한 spoke들을 랜덤하게 다시 pairing 하는 것이다. 즉 연결을 random 하게 하여서 최종적인 random graph가 생성되는 것이다.
이러한 configuration model은 clustering coefficient와 diameter, APL은 바뀔 수가 있어도 무조건 내가 생성한 모델과 degree distribution은 동일하게 생성될 수 있다.
cofiguration model의 randomly pairing의 방식은 switching으로 정의 된다. switching이란 한 쌍의 edge를 선택하고 교차하는 방법이다. 이 때 방향성은 유지 시켜야하는 것이 핵심이다.
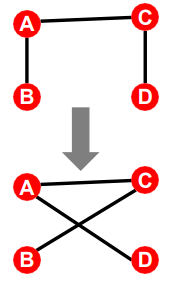
위 그림처럼 A->B, C -> D 형태로 되어있으면 A, C는 sender, B,D는 reciever의 역할을 한다. 따라서 이러한 역할은 유지한 상태로 switching이 이뤄져야하는 것이다.
따라서 swithcing은 Q*|E| 만큼 반복을 한다. 즉, 모든 노드에 대해서 반복을 한다. 그리고 이 반복을 convergence 될 때 까지 한다.
## Variation of motif concept
Direct 와 Undirected에 따라서 motif가 달라진다.
또한, 노드의 색깔에 따라 color vs uncolor로 해서도 motif가 달라진다
이러한 것들을 활용하여 feed forward loop와 bi-fan 쪽에서 활용이 되고 먹이 사슬에도 motif 분석이 활용된다
## Summary
다시 한 번 정리하면 다음과 같다.
1. 실제 그래프에서 각각의 pattern을 가진 subgraph를 count 한다.
2. configuration model 을 통해 생성한 random graph에서 각각의 pattern을 가진 subgraph를 count한다.
3. Z-score를 계산한다
4. 높은 Z-score를 가진 것에 대한 패턴에 대해서 분석한다
'Graph Mining' 카테고리의 다른 글
| Extract Subgraph Enumeration(ESU) (0) | 2021.12.07 |
|---|---|
| Graphlets (0) | 2021.12.07 |
| Small World (0) | 2021.12.06 |
| Random Graph (0) | 2021.12.06 |
| Network Properties (0) | 2021.12.06 |




댓글