## Random Graph
Random Graph는 그래프를 실제 세계와 비슷하게 생성을 하고, 이를 통해 내가 분석한 graph와 비교하기 위해서 생성을 한다. 즉, 평가지표를 위한 하나의 수단이다.
기존의 그래프 생성 방식에는 두가지가 있다
1. \( G_{nm} \) : n개의 노드와 m개의 edge가 있을 때 랜덤 그래프 생성. 이 때, uniform한 확률로 edge 를 뽑아내는 방식
2. \( G_{np} \) : 확률 p를 이용하여 원래의 edge 개수와 동일하게 선택하는 방식

예를 들어 위 그림과 같은 graph가 있다고 가정하자. 여기서 node는 4개 ,edge는 2개이다. 이러한 그래프에서 이 값을 갖고 fully connected된 그래프를 생각한다. 그리고 fully connected된 그래프에서 edge가 선택될 확률 p를 통해서 edge를 선택하는 것이다.
다시 정리하자면 4개의 노드로 구성된 fully connected graph에서 e의 개수 2에 도달할 때 까지 p의 확률로 edge를 선택하는 방법이다.
하지만 이러한 방식을 택하면 random graph의 Variance가 너무 커진다는 문제점이다. 즉, 너무 다양해진다는 것이다. 이렇게 되어버리면 내 그래프와 랜덤 그래프를 비교할 때 구별되는 특징을 정확히 파악을 할 수 없다는 문제가 생겨버린다.

이러한 \( G_np \)의 지표들을 보면 다음과 같다.
- Degree Distribution : 이항분포를 따름
- APL : O(log N)
- average clustering coef : \frac{\bar{k}}{n}
- GCC : k > 1 일 때 존재
하지만 결론적으로 말하면 G_np는 현실세계의 그래프(ex. MSN)과 다른 점이 있다. 바로 Degree Distribution과 average clustering coef 가 다른 문제점이다.

따라서 이러한 식이 어떻게 나왔는지 도출해보고, 왜 다른지 알아보자
## Degree Distribution (G_np)
G_np의 degree distribution은 앞서 언급한 것과 같이 이항 분포를 따른다. 이를 증명하면 다음과 같다.
$$ P(k) = {}_{n-1} C_k p^{k}(1-p)^{n-1-k} $$
전체 노드(자기 자신을 제외한 n-1)에서 k개의 노드를 선택할 경우의 수는 \( {}_{n-1} C_k \)이다. 그리고 그 노드끼리 연결되어 있을 확률은 \( p^{k} \) 이고 그리고 연결되어 있지 않을 확률은 \( (1-p)^{n-1-k} \) 이다. 따라서 이 확률을 모두 합치면 P(k)가 되고 이는 이항분포를 따르게 된다.
## Clustering Coefficient (G_np)
한 노드 i에 대해서 C는 \( C_{i} = \frac{e_{i}}{{}_{k} C_2} \) 이다. 이는 앞에서 설명했으므로 생략한다.
여기서 확률 p에 대해서 엣지가 연결될 기댓값은 \( E(e_{i}) = p {}_{k} C_2 \)가 나온다.( 기대값 = 실제값 x 확률)
이를 조금 상세하게 설명하자면 edge가 선택될 확률은 p이고 edge의 개수는 \( {}_k C_2 \) 이니까 이렇게 기대값이 형성이 된다.
그럼 이를 이용하여 C의 기대값을 구하면
$$ E[C_{i}] = \frac{ p {}_{k} C_2}{ {}_{k} C_2 } = p = \frac{ \bar{k} }{n-1} $$
가 된다. 이 값은 \( \frac{ \bar{k} }{n} \) 과 유사하므로 이로 정의한다.
여기서 p는 전체 노드의 개수에서 degree의 평균이 되는 것이니 \( \frac{ \bar{k} }{n-1} \)을 따른다고 정리할 수 있다.
## GCC(Giant Connected Componet)
GCC는 결론적으로 G_np에서 형성이 된다. \( p = \frac{k}{n-1} \rightarrow k = p(n-1) \) 라고 재정의할 수 있다.
다음과 같은 그래프를 보자
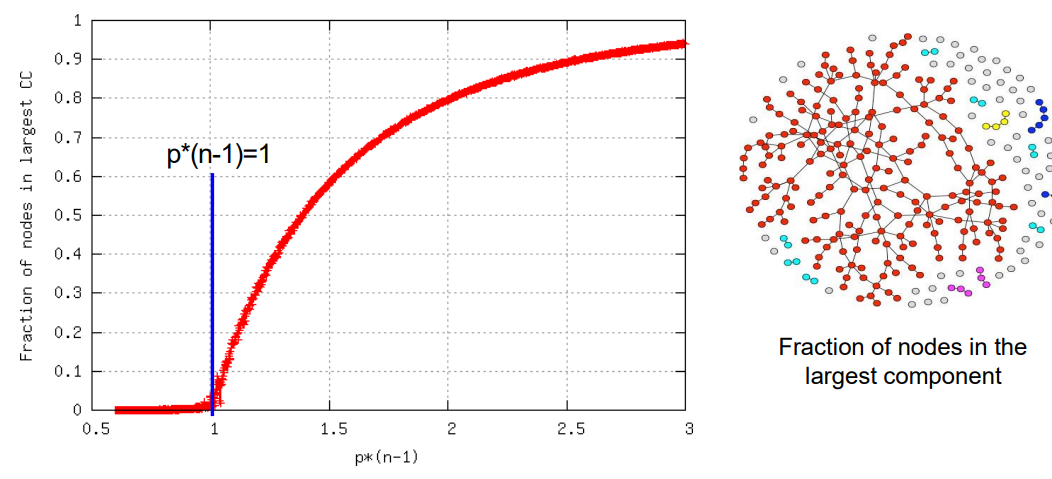
여기서 p*(n-1)은 k를 말하고 이게 증가한다는 것은 노드의 개수가 증가하거나 노드가 선택될 확률이 증가한다는 것이다. 즉, 노드와 노드가 서로 연결될 확률이 증가한다는 것이다. 이는 노드가 GCC안에 포함도리 확률이 높아진다는 것이다.
따라서 다음과 같은 그림에서 왼쪽의 그래프에 빨간색 노드로 연결된 것이 GCC이고 이는 k가 1이상일 때 GCC가 생성이 된다. plot은 실제로 실험한 G_np의 측정값이다.
따라서 이렇게 비교를 하다보면 위의 비교 그림과 같이 실제 그래프와 달라지게 된다. 앞서 말했듯이 Degree distribution과 clustering coefficient 가 달라진다. 왜 그럴까?
여기서 추측할 수 있는 한가지는 Degree와 관련되어 있다는 것이다. clustering coefficient에도 degree의 평균 값이 들어가 있기 때문에 degree와 연관되어 있다는 것을 추측할 수 있다.
MSN 네트워크의 특성을 보면 대부분의 노드들의 degree는 1이고 heavy tail(0.1%) 부분의 degree가 엄청나게 많은 형태를 띈다. 반면에 G_np 같은 경우는 모든 edge들이 uniform하게 degree를 갖는다. 따라서 이는 다를 수 밖에 없다.
정리하자면, G_np 는 실제 그래프에 비해 Clustering coefficient 가 매우 낮아서 real world의 그래프와 비교했을 때 다른 점이 있다. 이러한 이유는 G_np는 local structure를 반영하지 못하기 때문이다. local structure는 작은 부분들의 densly한 connected를 한다.(꼭 dense 아녀도 되는데 여기선 dense한 점을 반영 못하기 때문에 이렇게 말한 것)
즉, 부분적인 특성을 나타낼 수 없다는 것이 \( G_{np} \)의 문제점이다.
\( G_{np} \) 는 결국 틀렸지만, simple & fast 하게 생성할 수 있는 장점이 있다
'Graph Mining' 카테고리의 다른 글
| Graphlets (0) | 2021.12.07 |
|---|---|
| Subnetwork, subgraph, motif (0) | 2021.12.07 |
| Small World (0) | 2021.12.06 |
| Network Properties (0) | 2021.12.06 |
| Graph Mining 기초 (0) | 2021.12.06 |




댓글