## Graph Network 속성들
- Degree Distribution : P(k)
- Path Length : h
- Clustering coefficient : C
- Connected Component : s
## Degree Distribution
Degree의 개수의 분포를 나타냄
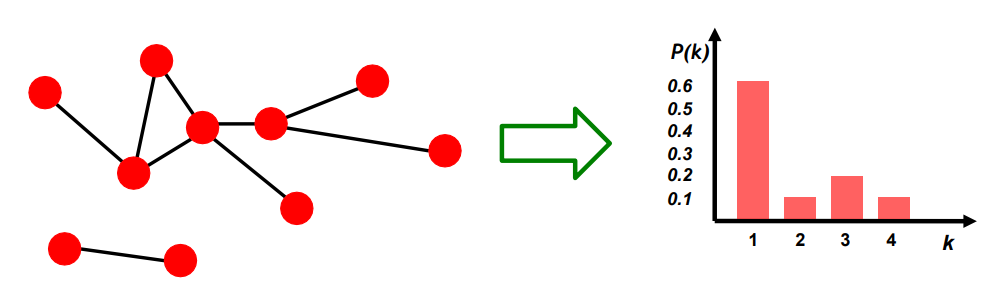
$$ P(k) = N_{k} / N $$
N = 총 degree의 개수, N_k = k번째 노드의 degree
## Path Length
A 노드에서 B 노드로 가기 위해 거쳐야 할 노드(or 엣지)들

A -> G로 가기 위해 ACBDCDEG 방법 등 여러가지 방법이 있음
여기서 파생되는 개념은 shortest path length(=distance)
크루스칼 알고리즘 처럼 가장 짧은 루트를 선택
여기서 Undirected와 Directed 여부에 따라 distance가 달라질 수 있음

edge가 연결되지 않은 경우는 \( \infty \)로 표현. undirected graph에서 \( h_{A,C} \)는 1이 된다. 그러나 directed에선 2가 된다.
### APL(Average Path Length)
APL은 평균 경로 거리로 2개의 node를 pair로 뽑는 nC2의 경우의 거리를 모두 구해서 평균내는 것이다.
즉 수식은 다음과 같다.
$$ \bar{h} = \frac{1}{2E_{max}} \Sigma_{i,j \neq i} h_{ij} $$
위 식은 undirected graph 기준이고 \( E_{max} \) = nC2이다. 따라서 중복으로 세지는 edge가 있기 때문에 2로 나눠준다.
하지만 APL은 연결이 되지 않은 isolated node를 고려하지 않기 때문에(왜냐하면 isolated node와 거리는 무한대이므로) APL이 높으면 isolated node가 많은지도 고려해야한다.
### Diameter
diameter는 노드-노드 거리 중 가장 긴 것을 말한다(최대 거리)
## Clustering Coefficient
Clustering Coefficient 는 얼마나 노드들이 dense하게 묶여 있는지 판단하는 것이다. 즉, 그래프가 얼마나 dense하게 연결되어있는지를 판단하는 것이다.
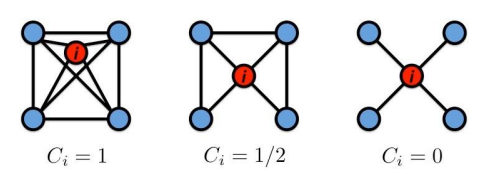
식은 다음과 같다. 노드 하나의 기준으로 적으면
$$ C_{i} = \frac{2e_{i}}{k_{i}(k_{i}-1)} $$
위 식에서 k는 degree의 수, e_i는 다른 edge 들이 얼마나 엮여 있는지를 나타낸다. 따라서 이렇게 한 노드의 기준으로 Clustering Coefficient를 구하고 이를 모든 노드 N에 대해서 나눠서 Graph에 대한 Clustering Coefficient를 구한다.
위의 예시에서 두번째 그래프를 기준으로 보자. 두번째 그래프에서 node i의 degree로 k_i = 4이다. 그리고 주변의 node들의 edge는 총 3 이므로 e_i 는 3이다. 따라서 (2*3)/(4*3)으로 1/2 가 도출된다. 3번째 그래프는 e_i가 0이므로 C_i도 0이 된다.
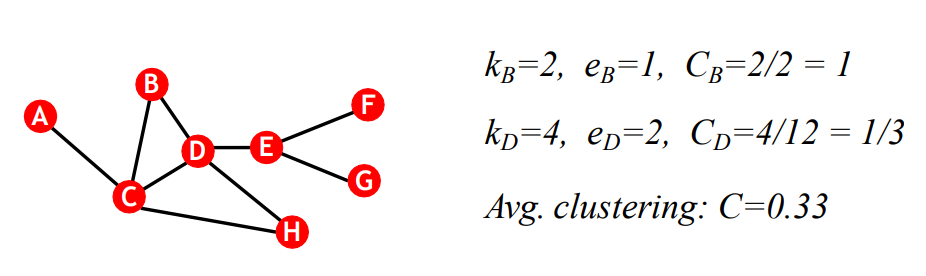
이해가 안되면 위 예시를 통해 상세하게 계산을 해보면 된다.
## Connectivity
connectivity는 연결된 노드들 중 가장 연결성(노드의 개수)이 가장 큰 것을 판단하는 것이다.
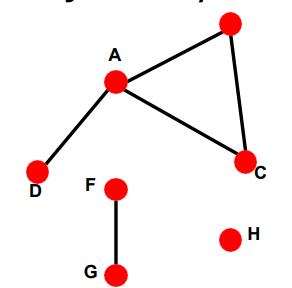
위 그래프에서 connectivity를 계산하면 위 쪽은 노드가 4개여서 4, 밑에 F-G는 노드가 2, H는 노드가 1로 따라서 위 그래프의 connectivity s=4가 된다.
정리하자면 다음과 같다
- Degree distribution \( P(k) \) : 그래프의 종합적인 degree 분포를 알 수 있음
- Path Length \( h \) : APL을 통해 grpah의 dense한 정도를 파악할 수 있다. 단, isolated node를 고려해야함
- Clustering Coefficient \( C \) : 얼마나 노드들이 Dense하게 묶여져 있는지
- Connected Components \( s \) : 가장 높은 connected component가 무엇인지
'Graph Mining' 카테고리의 다른 글
| Graphlets (0) | 2021.12.07 |
|---|---|
| Subnetwork, subgraph, motif (0) | 2021.12.07 |
| Small World (0) | 2021.12.06 |
| Random Graph (0) | 2021.12.06 |
| Graph Mining 기초 (0) | 2021.12.06 |




댓글