본 글은 인천대학교 최대진 교수님의 강의에 기반하여 작성하였습니다
## Graph Mining
Large-Scale의 데이터를 다룰 때 통계치를 기반으로는 한계가 있다. 이를 극복하기 위해 그래프를 이용하여 유의미한 결과를 추출하는 것을 말한다.
대표적인 예시 : Edge가 가장 모여있는 Community를 찾는 것, 페이스북 사람들의 연결관계, 추천시스템
## Graph
Graph G = (V,E,W)로 이뤄져 있다. 여기서 대문자 V,E,W는 모두 집합의 형태이다.
- V = Vertex set (node 집합)
- E = Edge set
- W = Weight set
Graph Data structure : 엔티티 간의 관계, p2p network(path2path network)
## Graph Type
- Undirected Graph : edge에 방향성을 가지지 않음 (ex. 페이스북 친구) \( (A,B) = (B,A) \)
- Directed Graph : edge에 방향성을 가짐 (ex. 인스타 팔로우 팔로잉) \( <A,B> \neq <B,A> \)
- Unweighted Graph : 모든 edge에 대해서 weight가 같음
## Degree
간선(Edge)의 개수
- Undirected Graph

위 그래프에서 \( node_{1} \)의 degree = 2, \( node_{2} \) 의 degree = 3

Direct Graph는 방향성이 있기 때문에 In-degree와 Out-degree로 나누어짐
In-degree : 들어오는 edge의 수, out-degree : 나가는 edge의 수
따라서 위 그래프에선 \( node_{1} \)의 in-degree = 1, out-degree = 2, \( node_{2} \) in-degree= 1, out-degree = 0
## Graph의 저장형태
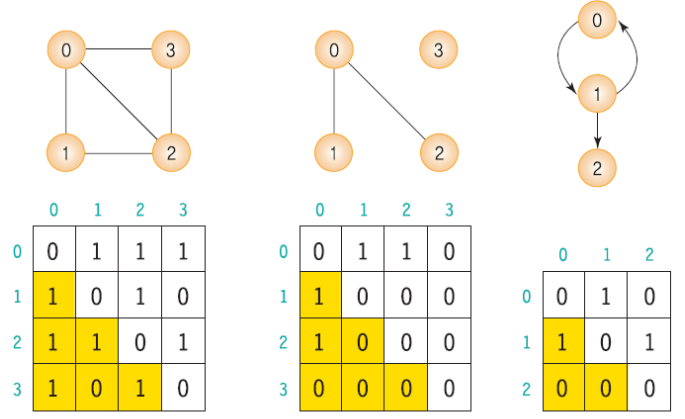
adjacent matrix 형태로 저장함. matrix를 M이라고 할 때 node_i와 node_j 가 연결되어 있으면 M[i][j] = 1, 아니면 M[i][j] = 0
## Graph와 Tree의 차이
Tree는 모든 노드가 연결이 되어있고, Cycle이 없음
'Graph Mining' 카테고리의 다른 글
| Graphlets (0) | 2021.12.07 |
|---|---|
| Subnetwork, subgraph, motif (0) | 2021.12.07 |
| Small World (0) | 2021.12.06 |
| Random Graph (0) | 2021.12.06 |
| Network Properties (0) | 2021.12.06 |




댓글