앞선 포스팅에서 행렬식 determinant를 계산할 때 det A = 0 이면 역행렬이 존재 하지 않는다고 하였다. 이를 determinant의 관점이 아닌 Ker 과 Rank 의 관점에서 한 번 보자
## Square Matrix에서 역행렬이 존재하기 위한 조건
Square matrix A에서 ker A가 원점 0뿐이면 즉, 0차원이면 차원 정리에 따라 rank A = n 이라는 말과 같다. 이렇게 되면 단사인 경우가 된다. 단사가 되면 역행렬은 존재하는 상태가 된다. 이에 반해 전사일 경우가 되면 역행렬이 없는 경우가된다.
이렇게 설명하니 뭔 말인가 싶지만 그러면 각각 같은 말을 나열하면서 정리해보겠다.
A가 n차 square matrix일 때 (square matrix만이 역행렬 존재) 역행렬이 조건
- A는 단사로 mapping
- Ker A가 원점 뿐이다
- dim Ker A = 0
- A는 전사로 mapping
- Im A 가 n차원 공간 전체
- rank A = dim Im A = n
- \( a_1 ... a_n \) 이 선형독립
- Ax = 0 이 되는 것은 x = 0 뿐이다.
- \( \det A = \neq 0 \)
- A가 고윳값(eigen value) 0을 갖지 않는다
- \( A^T \) 가 정칙 행렬이다
- 어떤 n 차원 벡터 y에서도 y = Ax 가 되는 x가 딱 한 개 있다.
이를 모두 만족하면 역행렬이 존재한다.
그럼 이와 반대되는 조건 즉, 역행렬을 가지지 않을 조건은 다음과 같다.
- square matrix가 아닌 n차원 벡터 y 이면 y = Ax 가 되는 x가 없다. 또한, x의 값이 여러개 있는 경우
- A 는 특이행렬
- A의 사상은 단사가 아니다
- Ax = 0 이 되는 x \( \neq 0 \) 이 존재
- Ker A가 원점 o 뿐이 아니다
- dim Ker A > 0
- A의 열벡터 \( a_1 , ... , a_n \)이 선형 종속
- A의 사상은 전사가 아니다
- Im A 가 n차원 공간 전체가 아니다
- rank A = dim Im A < n
- det A = 0
- A가 eigen value 0을 가진다
- 이러한 A를 \( A^T \)로 치환한 것
## 역행렬이 없을 때
역행렬이 존재하지 않을 때 문제를 어떻게 풀까? 일단 두가지 경우가 존재한다
해가 존재하지 않는 경우와 해가 무수히 많은 경우가 있다.
여기서 먼저 해가 무수히 많은 경우를 보자. 이 때 먼저 어떻게든 해를 하나 구한다. 이를 \( x_0 \) 라고 하고 이를 특해라고 부른다. 그리고 이 특해에 Ker A에 속하는 벡터 z를 여러가지 형태로 변형하여 \( x_0 + z \) 형태로 여러가지 모든 해를 구한다. 이를 일반해라고 하고, 이를 Ax = y 의 형태로 나타낼 때의 해는 특해 + 일반해 의 구조를 갖는다.
즉 이를 식으로 나타내면 다음과 같다.
$$ x = x_0 + c_1 z_z + ...+ c_k z_k $$
이런 식으로 역행렬이 없고 해가 무수히 많은 경우에서 해를 구하는 방법이다.
구체적인 예시를 통해 다시 봐보자
## 해가 존재하지 않는 경우
예를 들어 다음과 같은 방정식이 있다 하자
\begin{align} 2x_1 - 4x_2 = -2 \\ 4x_1 - 5x_2 = 2 \\ 5x_1 - 9x_2 = 1 \end{align}
이러한 방정식을 기본행 연산을 통해 조작하면 다음과 같은 행렬이 나오게 된다.
\begin{bmatrix} 1 & 0 & 3 \\ 0 &1 & 2 \\ 0 & 0 & 4 \end{bmatrix}
이를 연립 방정식 형태로 나타나면 \( x_1 = 3 \ x_2=2 \ 0=4 \) 처럼 나타난다. 이 결과에서 0 = 4 처럼 말도 안되는 식이 나오면 이는 해가 없다. 라고 판단한다.
## 무수히 많은 해가 존재하는 경우
\begin{align} -x_1 + 2_x2 - x_3 + 2x_4 = 6 \\ 3x_1 - 4x_2 - 3_x3 - 2x_4 = -4 \end{align}
이와 같은 식이 있을 때 이를 행렬로 나타내면 다음과 같다.
\begin{bmatrix} -1 & 2 & -1 & 2 & 6 \\ 3 & -4 & -3 & -2 & -4 \end{bmatrix}
이를 기본행 연산으로 조작하면
\begin{bmatrix} 1 & 0 & -5 & 2 & 8 \\ 0 & 1 & -3 & 2 & 7 \end{bmatrix}
그리고 이 matrix를 연립방정식으로 나타내면
\begin{align} x_1 - 5x_3 + 2x_4 = 8 \\ x_2 -3x_3 + 2x_4 = 7 \end{align}
이렇게 되고 \( x_3 = s, x_4 = t \)로 두고 해를 구하면
\begin{align} x_1 = 5s-2t+8 \\ x_2 = 3s-2t+7 \\ x_3 = s \\ x_4 = t \end{align}
이렇게 나온다. 이런 방식으로 미지수로 두면서 해를 구하게 된다.
즉 해를 구하는 방식은 다른 해 구하는 방식과 동일하게 기본행 연산으로 행사다리꼴 형태로 조작 후 해를 미지수로 둔 다음 방정식을 풀면 된다.
하지만 이렇게 하다보면 행사다리꼴 형태로 정확하게 안되는 경우가 발생한다.
예를 들어 다음과 같은 형태의 matrix를 보자
\begin{bmatrix} 1 & 0 & 5 & 4 & 4 \\ 0 & 1 & 2 &3 & 2 \\ 0 & 0 & 0 & 3 & 6 \end{bmatrix}
이러한 경우 3번째 행의 3번째 열 값이 0이 아닌 값이 나와야되는데 4번째 열에서 나오게 된다. 이러면 행사다리꼴 형태로 풀 수가 없다. 이를 해결하기 위해 다음과 같은 trick을 쓴다.
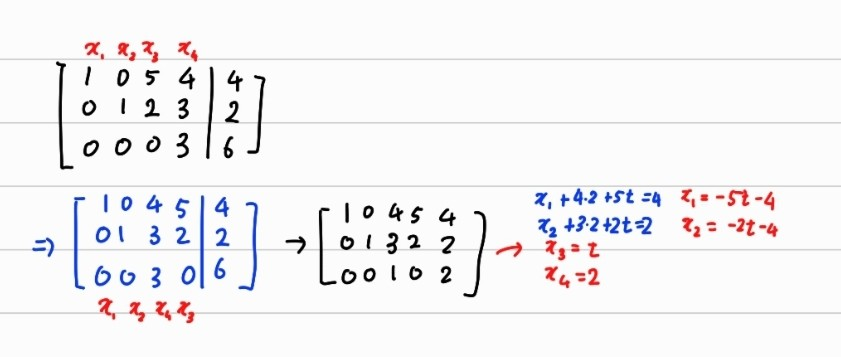
이런 식으로 열을 서로 바꿔주고 바뀐 열을 기록해 놓고 이에 따라서 풀면 된다.
'Linear Algebra' 카테고리의 다른 글
| 대각화(2) (0) | 2022.01.20 |
|---|---|
| 대각화(1) (0) | 2022.01.04 |
| Rank 계산 (0) | 2022.01.02 |
| 차원 정리 및 Rank (0) | 2021.12.31 |
| 정칙행렬이 아닌 경우 (0) | 2021.12.28 |




댓글