Standalone DeepLearning 강의를 기반으로 작성되었습니다.
https://www.youtube.com/watch?v=is_Vw-aJMg4&list=PLSAJwo7mw8jn8iaXwT4MqLbZnS-LJwnBd&index=5
## Binary Classification

예를 들어 어떤 사진이 있을 때, 그 사진이 라벨링이 되어있을 때 즉, 이 사진은 고양이 사진이라고 라벨링이 되어있을 때 x:y 가 mapping 되어있을 때 이를 바탕으로 훈련을 시킨 것을 supervised learning이라고 한다. 그리고 이러한 output 값이 discrete(이산적)인가 continuous(연속적)인 것에 따라 문제를 classification, regression이라고 정의한다.
그 중 Binary Classification은 개냐 고양이냐 처럼 예측할 클래스가 두개인 것을 Binary classification이라고 말한다.
## Binary Classification Hypothesis
문제를 예로 들어 설명하겠다. 공부 시간에 따른 불합 여부에 대해서 분석하고자 한다. 이 때, 합격은 1 불합은 0 이라고 하자
이러한 문제를 linear regression으로만 해결할 수 있을까?
아니다.

위 그림을 보면 기존의 regression으로 빨간색 점과 파란색 점을 구분할 수 있다. 만약에 study hour는 기존 학생들보단 길고 합격인 사람이 새롭게 유입됐다고 하자. 이럴 경우에는 regression 의 기울기가 바뀌어야하는데 이렇게 되면 파란색 점인 fail한 사람들을 분리한 것도 분류를 못할 경우가 생길 수 있다. 따라서 기존의 linear regression이 아닌 새로운 classification 모델을 만들어야한다.
따라서 이러한 분류 문제를 해결하기 위해 sigmoid function을 도입한다.

function G는 기존의 linear regression의 hyphothesis 식 H(x) = Wx + b 에 classification을 위한 함수 G라는 처리를 해서 해결하자라는 의미로 나온 함수이다. 즉 classification 문제는 H(x) = G(Wx+b) 로 해결할 수 있게 하는 것이다.
sigmoid function은 0~1 사이의 범위를 가진다.
따라서 classification을 위한 hypothesis는 다음과 같이 정의된다.

sigmoid function에 regression 식 Wx+b를 넣은 것과 같다.
(WX 앞에 -를 붙여줘야한다. 오타..)
## Binary Classification Cost
Regression에선 Cost function을 MSE로 사용하는데, 이 cost function을 classification에 그대로 적용할 때의 문제점은 무엇이 있을까?

regression mse에선 local minima 가 없이 매끄럽게 진행되는 반면, classification은 local minima(saddle point)가 자주 보일 수 있다. 이렇게 되면 학습을 진행하여도 학습이 효율적으로 안되고 아예 안되는 경우가 발생할 수 있다.
따라서 이러한 문제점을 해결하기 위해 Cross Entropy라는 개념을 도입한다.

이 식에서 P(x)는 실제 확률이고, Q(x)는 예측확률이다.
예를 들어서 Q(x)는 0.01 이고, P(x)는 1이라고 가정하자. 이러한 경우에는 값이 매우 커지게 된다. -log 함수를 생각해보면 된다. 그럼 Q(x)가 0.99이고 P(x)가 1이라고하면 H(P,Q)의 값은 매우 작아진다.
따라서 예측을 못하면 못할수록 커지는 값이 Cross Entropy이다.
Cross Entropy를 이용한 Cost function을 정의하면 다음과 같다.

처음 식에서 i는 i 번째 데이터를 말한다. m 은 데이터의 총 개수를 말한다.
따라서 cost(W)는 각 데이터의 cost를 계산하고 이를 평균낸 것이다.
cost function은 두번째 식처럼 나타내진다. y=1 일 때에는 cost는 -log(H(x)), y=0 일 떄는 -log(1-H(x)) 이다.
두번쨰 식을 풀어 쓴 것이 세번째 식처럼 된다.
## Multinomial Classification
Multinomial Classification이란 분류하려는 class의 개수가 2개가 아닌 여러개인 경우를 말한다. 예를 들면 MNIST 데이터셋을 생각할 수 있다. 이러한 경우엔 Binary Classification과 동일하게 진행해도 문제가 없을까?
예를 들어 출석과 공부 시간에 따라서 학점을 분류 예측하는 경우를 생각해보자

sigmoid function에서 Wx+b가 0.5가 되기 위해선 Wx + b = 0 이 되어야한다. 따라서 이를 풀면 w1x1+w2x2+b=0 이 된다. 그래서 이러한 직선의 방정식을 구하고 보라색 선 중 하나의 선이 나오게 된다.
하지만 보라색 선 두개로 class를 분류할 수 있지만 하나의 직선으로는 절대로 A,B,C를 알맞게 분류할 수 없는 상황이다. 따라서 Binary Classification과 다른 hypothesis를 정립할 필요가 있다.
## Multinomial Classification Hypothesis
앞서 binary classification hypothesis를 정의할 때처럼 linear regression 모델에 어떠한 함수 G를 씌우면 binary classification이 되는 것처럼 이도 동일하게 진행한다.
그림으로 설명하겠다.

앞서 언급한 예를 바탕으로 x1 = study hour, x2= attendence이다. 그래서 x1, x2를 input 값으로 넣으면 y1,y2,y3 라는 값이 나오게 되게 만든다. 그런데 이를 y1,y2,y3로 반환하게 되는데 이를 어떠한 함수 G를 거쳐서 y1 이 나올 확률, y2가 나올 확률, y3가 나올 확률로 만드는 것이다. 그러면 가장 높은 확률 값을 가진 것을 선택하면 input 값에 대한 예측 class를 구할 수 있기 때문이다.
이러한 함수 G는 softmax function을 사용한다.

이를 설명하면 총 j 개의 class가 있을 떄 i 번째의 클래스가 나올 확률 값을 계산하는 것이다.
예를 들어 A 학점을 받을 확률을 계산한다고 해보자. 이 softmax function을 풀어쓰면 다음과 같다.
e^(y_1) / (e^(y_1)+e^(y_2)+e^(y_3))
## Multinomial Classification Cost
binary classification과 동일하게 CrossEntropy를 정의한다.

S(y)는 predict한 확률 값이고(softmax를 통과한 값) y는 실제 확률 값이다.
binary classification 때는 y와 1-y를 나눠서 분리하지만(이진확률 분리 q = 1-p) multinomial일 때는 전체적인 확률값으로 나오기 때문에 sum을 하여 계산하게 된다.
## Conclusion
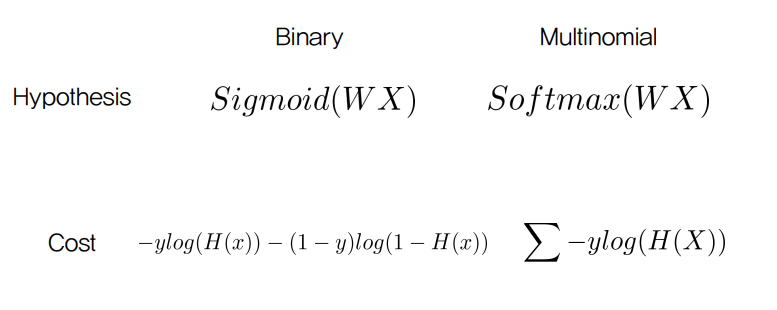
Binary 일 때 linear regression에 씌우는 값은 sigmoid이고 mutlinomial일 땐 softmax function이다.
그리고 cost function은 동일하게 cross entropy 를 사용한다.
'딥러닝 기초' 카테고리의 다른 글
| Advanced Optimizer than SGD (0) | 2021.08.14 |
|---|---|
| Overfitting, Regularization (0) | 2021.08.01 |
| 코드에서 파라미터 최적화 (0) | 2021.07.28 |
| MultiLayer Perceptron (0) | 2021.07.26 |
| History of DeepLearning (0) | 2021.07.21 |



댓글