이 글은 https://www.youtube.com/watch?v=oOQCrm4Vemo&list=PLSAJwo7mw8jn8iaXwT4MqLbZnS-LJwnBd&index=7&t=652s
영상을 기반으로 작성하였습니다.
## Solving XOR problem with MLP

위 그림에서 MLP의 input layer는 input 값이 들어가게 된다. 그리고 hidden layer에서 하나의 동그라미는 hidden unit이라고 한다. 그리고 MLP에서 화살표의 의미는 가중치를 곱해주는 것이다. 또한 가중치를 곱한 후에 activation function을 통과한다.
## XOR
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
이러한 XOR 문제를 해결하기 위해 다음과 같이 MLP를 구성한다.
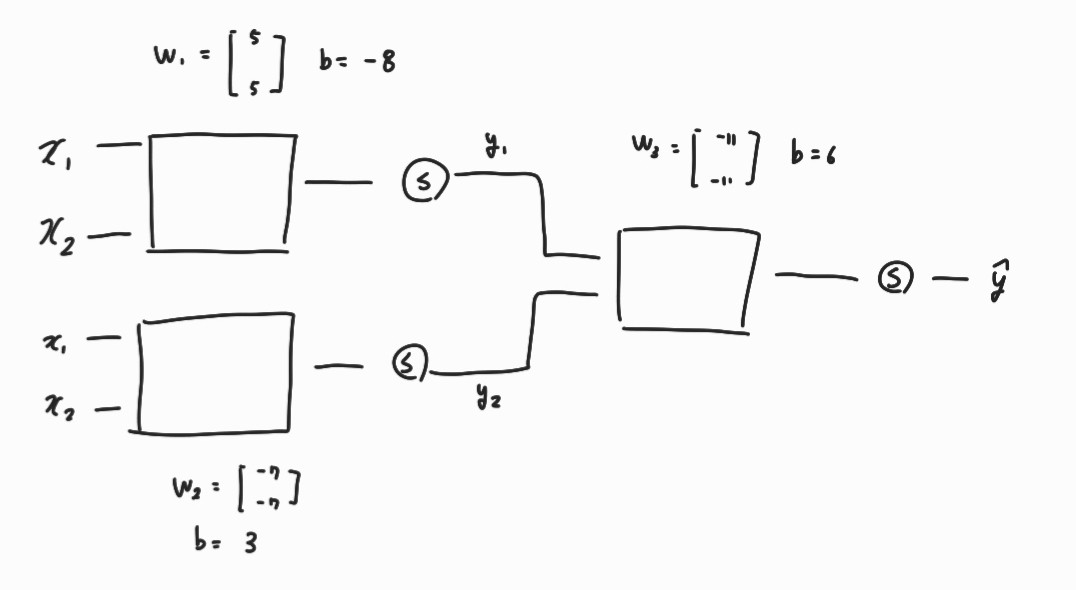
위 그림에서 S는 sigmoid function이고 왼쪽에 있는 네모를 위에서부터 편의상 1번 layer, 아래에 있는 네모를 2번 layer, 오른쪽에 있는 layer를 final layer라고 칭한다.
input 값으로 \(x_{1} = x_{2}=0 \) 을 대입한다. 1번 layer에 통과 시켜보면 -8이 되고 그 다음엔 sigmoid 층을 통과하면 0에 근사하는 값이 된다. 그리고 2번 layer에 통과 시키면 1에 근사하는 값이 나온다. 그리고 여기서 도출된 값을 final layer에 넣어주면 -5가 나오고 이를 sigmoid에 넣어주면 0에 근사한 값이 나온다. 따라서 target 값과 output 값이 일치하게 된다. 이러한 방식으로 모두 (0,0),(0,1),(1,0),(1,1) 을 모두 해주면 다음과 같은 표가 도출된다.
| x1 | x2 | y1 | y2 | \( \hat{y} \) | y |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 |
모두 정확하게 예측을 함을 알 수 있다.
이러한 MLP 구조에서 어떻게 bias와 weight 를 정하고 어떻게 훈련할 수 있을까?
이러한 해답은 backpropogation에 있다.
## Backpropogation
MLP Backpropogation의 핵심은 Chain Rule이다. Chain rule을 한 번 손으로 풀어보자
예를 들어 \( f = g+b, g = wx \) 라고 하자. 이를 합치면 \( f = wx +b \) 가 나온다.
이를 그림으로 표현하면 다음과 같다.

backpropogation을 하기 전에 feedforward를 구해보자.
\( w=-2, x = 5, b=3 \) 이라고 하자. 그러면 \( g=10 \)이 되고 \(f=-7\)이 된다. 따라서 feedfoward는 그냥 수식으로 따라가기만 하면 된다.
그러면 이를 기반으로 backpropogation을 구해보자
우선 각각의 편미분 값을 구해보자.
\( \frac{\partial f}{\partial g} = 1, \frac{\partial f}{\partial b} = 1, \frac{\partial g}{\partial w} = x \frac{\partial g}{\partial x} = w\) 이다.
그러면 이를 chain rule에 의해서 \( \frac{\partial f}{\partial w} = \frac{\partial f}{\partial g} \dot \frac{\partial g}{\partial w} = 1 \times x = x \) 가 도출된다. 따라서 이를 기반으로 계산을 해서 그림을 그리면 다음과 같은 그림이 도출된다.

이런 원리를 이용하여 backpropogation을 수행하고 mlp를 훈련 시킬 수 있다.
'딥러닝 기초' 카테고리의 다른 글
| Advanced Optimizer than SGD (0) | 2021.08.14 |
|---|---|
| Overfitting, Regularization (0) | 2021.08.01 |
| 코드에서 파라미터 최적화 (0) | 2021.07.28 |
| History of DeepLearning (0) | 2021.07.21 |
| Binary/Multi Classification (0) | 2021.07.18 |



댓글