본 글은 https://www.youtube.com/watch?v=a5R4gL1ObP8&list=PLSAJwo7mw8jn8iaXwT4MqLbZnS-LJwnBd&index=16
위 동영상을 바탕으로 하였습니다.
## Batch Stochastic Gradient Descent
Gradient Descent 를 식으로 쓰면 다음과 같다,
$$ \theta = \theta - \eta\triangledown J(\theta) $$
여기서 \( \theta \)는 모델에 설정된 파라미터를 말하고 \( \eta \)는 learning rate, \( J(\theta) \) 는 loss function을 의미한다.
이는 파라미터 \( \theta \) 에서 loss 에 있는 파라미터 \( \theta \) 에 대한 loss를 계산하고, 거기에 learning rate를 곱해서 빼주는 것이다. 이를 반복하다 보면 global minma에 도달한다는 것이다.
이러한 gradient descent는 두가지로 나눠지는데 첫번째는 Batch Gradient Descent 이다.
Batch Gradient Descent는 한 번 step을 밟을 때 training set 전체에 대해서 Gradient를 계산하는 것이다. 이러면 메모리가 너무 많이 소요되고, 그리고 이를 한 번에 계산을 할 때 너무 많은 계산을 하니 너무 느려서 optimize가 느려진다.
따라서 이러한 단점을 보안한게 Stochastic Gradient Descent(SGD) 이다.
이는 Batch Gradient Descent 처럼 training set 모두를 계산하는 것이 아니라 mini-batch로 하여 그 부분만 계산을 하고 Gradient 를 계산하게 되면서 더 빠르게 계산이 된다. 이는 확률적으로 미니 배치가 설정되면서 계산이 되므로 Stochastic이라고 한다. 이렇게 확률적으로 계산하게 되면 local minima에 빠질 확률이 적어진다.
## Advanced Gradient Descent
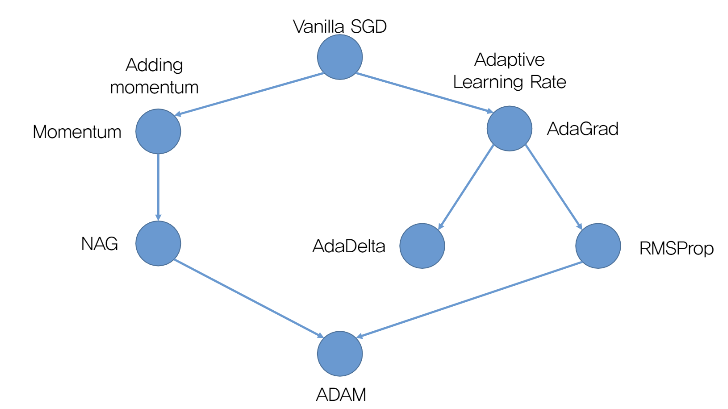
위 그림은 optimizer의 발전 계보이다. 왼쪽으로 가는 것은 momentum 개념을 통해서 적용하고 그 momentum을 변형하여 발전한 것이고, 오른쪽에 뻗어 있는 노드는 학습률을 변경해서 발전시킨 것이다.
이러한 발전을 하게 된 계기는 SGD는 local minma에 빠질 경향이 있다는 것이다. 따라서 이러한 경우를 해결하기 위해 나온 것이 momentum이다. momentum을 적용한 식은 다음과 같다.
$$ \theta = \theta - v_{t}$$
$$ v_{t} = \gamma v_{t-1} + \eta \triangledown_{\theta} J(\theta) $$
여기서 \( v_{t} \)는 속도로 momentum을 나타낸다. 그리고 v_{t} 식에서 \( \gamma \)는 decay instance로 계속 양수의 값을 더해지는 것을 방지하기 위한 것이다. 따라서 \( \gamma \)는 0~1 사이의 값이다.
따라서 이러한 momentum을 통해서 local minimum에 빠지는 것을 방지할 수 있다. 또한, 빠르게 global minimum에 수렴할 수 있다는 장점이 있다.
하지만 이러한 momentum 기법도 단점이 있다. Local minimum에서 벗어날 수 있다는 장점이 있지만 속도라는 관성때문에 global minimum 근처에서 왔다갔다 하다가 수렴을 하게 된다. 즉, 더 빠르게 수렴이 안된다는 것이다.
이러한 문제를 해결한 것이 Nesterov Accelerated Gradient(NAG) 이다. 식은 다음과 같다.
$$ \theta = \theta - v_{t} $$
$$ v_{t} = \gamma v_{t-1} + \eta \triangledown_{\theta} J(\theta - \gamma v_{t-1}) $$
이를 그림을 통해 설명하겠다.

momentum 방식은 gradient 에서 구한 방향과 momentum에서 구한 방향 벡터를 합하여서 진행하는 방식이었다.
그러나 NAG에선 momentum에서 구한 방향으로 step으로 진행하고 실제 출발점에서 gradient 를 계산하는 것이 아니라 momentum으로 진행한 방향에서 gradient를 계산해서 목표점으로 도달하게 되는 것이다.
수식에서 momentum과 바뀐점은 loss function의 시작점이다. 즉, \( \theta \) 에서 momentum을 뺀 값의 loss function의 기울기를 구하는 것이다. 따라서 이를 통해 global minima를 통해 더 빠르게 수렴이 가능하다.
그러나 NAG에서도 문제점이 있다. 바로 step size 마다 learning rate가 모두 동일하다는 것이다. 따라서 이를 반영하여 새로운 방법을 반영한 것이 AdaGrad이다.
$$ \theta_{t+1} = \theta - \frac{\eta}{\sqrt {G_{t} +\epsilon }} \cdot \triangledown_{\theta} J(\theta_{t} )$$
$$ G_{t} = G_{t-1} + ( \triangledown_{\theta} J(\theta_{t} )) ^{2} $$
위 식은 learning rate에 변수를 나눠서 learning rate가 변하게 된다. 여기서 변하게 하는 \( G_{t} \)는 전의 \(G_{t-1} \)에 gradient의 제곱을 더한 값이다. 그리고 위 식에서 동적인 learning rate에 기울기를 행렬곱이 아닌 원소별로 곱하는 것임을 유의해야한다. 이 때 learning rate는 각각의 원소마다 값이 달라서 각각의 위치마다 learning rate의 값이 달라진다.
하지만 이러한 AdaGrad도 하나의 문제점이 있는데 \( G_{t} \)의 값이 step이 지나면 지날수록 너무 커져서 무한대로 발산하게 되고 이는 learning rate가 0이 되는 문제가 발생한다. 따라서 이를 해결하기 위해 나온 것이 RMSProp 이다.
$$ \theta_{t+1} = \theta - \frac{\eta}{\sqrt {G_{t} +\epsilon }} \cdot \triangledown_{\theta} J(\theta_{t} )$$
$$ G_{t} = \gamma G_{t-1} + (1- \gamma)( \triangledown_{\theta} J(\theta_{t} )) ^{2} $$
\( \gamma \) 는 앞서 설명했듯이 decay instance 값으로 규제 효과가 있다.
다음으로 AdaDelta이다. 식은 다음과 같다.
$$ \theta_{t+1} = \theta_{t} - \triangle_{\theta} $$
$$ \triangle_{\theta} = \frac{\sqrt{s+\epsilon}}{\sqrt{G+\epsilon}} \cdot J(\theta_{t}) $$
$$ s_{t+1} = \gamma s_{t} + (1 - \gamma) \triangle_{\theta} $$
$$ G_{t+1} = \gamma G_{t} + (1- \gamma) (\triangledown_{\theta}J(\theta_{t})) ^{2} $$
식이 여러개로 섞여 있지만 거의 기존에 나왔던 방법을 합친 느낌이라고 생각하면 된다. 여기서 약간 다른 점은 decay에 기울기값을 곱한 것이 아니라 파라미터의 변화량을 곱했다는 점이다.
s를 고려한 이유는 기존엔 Gradient를 빼는 방식으로 하였지만 이게 문제점이라는 지적이었다. 왜냐하면 이는 loss function에서 parameter theta로 미분한 것이기 때문에 이는 parameter를 u라고 했을 때 u의 역수인 것이다. 따라서 이는 맞지 않다고 지적을 하였다. 따라서 이를 해결하기 위해 \triangle_{\theta}를 정의하고 단위를 맞춰준 것이다.
마지막으로 많이 쓰이는 Adam 이다.
Adam은 지금까지 나왔던 알고리즘들의 장점을 합쳐놓은 것이다. Adam의 식은 다음과 같다.
$$ m_{t} = \beta_{1} m_{t-1} + (1-\beta_{1} )g_{t} $$
$$ v_{t} = \beta_{2} v_{t-1} + (1-\beta_{2} ) g_{t} ^{2} $$
$$ \hat{m_{t}} = \frac{m_{t}}{1-\beta_{1}^{t}}$$
$$ \hat{v_{t}} = \frac{v_{t}}{1-\beta_{2}^{t}} $$
$$ \theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{\hat{v_{t}} + \epsilon } } \hat{m_{t}}$$
위 식에서 \( g_{t} \)는 loss의 기울기이고, momentum은 \( m_{t} \)이다. 그리고 \( v_{t} \)는 adaptive learning rate를 위한 변수이다. 그리고 마지막에 있는 식이 왜 존재해야하는지 이유를 설명하겠다. 실제로 시작할 때 \( \beta_{1} \beta_{2} \)는 1에 가까운 값으로 시작된다. 이러면 \( m_{t} \)는 커지고 \( v_{t} \)는 작아져서 첫 스텝이 너무 큰 경우가 발생하게 된다. 따라서 이를 작은 값을 나눠줌으로써 처음에 너무 큰 step으로 진행되는 것을 막을 수 있다.
'딥러닝 기초' 카테고리의 다른 글
| Advanced Architectures of CNN (0) | 2021.08.21 |
|---|---|
| Basic of Convolution Neural Network (0) | 2021.08.15 |
| Overfitting, Regularization (0) | 2021.08.01 |
| 코드에서 파라미터 최적화 (0) | 2021.07.28 |
| MultiLayer Perceptron (0) | 2021.07.26 |



댓글