## Vector
벡터는 기본적으로 종벡터 형식으로 표현한다. ex) \( (1,2)^T \)
이러한 벡터로 이뤄진 것을 벡터공간(Vector space) 라고 한다.
벡터 공간을 나타내면 다음 사진과 같다.

벡터는 방향성 해석을 중요시 한다. 따라서 위 그림에서 보면 A-> B 로 가는건 \( \vec{a} \) 로 나타낸다. 그래서 이런 방향성을 생각해서 vector space에서 \( \vec{a} + \vec{b} \) 를 계산하면 A -> C 로 가는 선이 된다.
## 기저(biasis)
기저 (biasis)는 어떤 벡터공간 V의 벡터들이 선형독립이면서 벡터공간 V 전체를 생성할 수 있다면 이 벡터들의 집합을 말한다.
즉, 선형 결합으로 이뤄지고 유일한 해를 가질 때 biasis라고 한다.
선형 결합은 공간 안에 있는 \( \vec{v} \) 가 \( x_n\vec{e_n} \)의 합으로 이뤄진 것을 말한다.
## 차원(Dimension)
차원은 기저 벡터의 개수를 말한다.
차원 = 기저 벡터의 개수 = 좌표의 성분 수
## 행렬(Matrix)
기본적인 내용은 생략하고 핵심만 적으면
### 기본 성질
- n x n matrix A,B가 임의의 vector x에 대해 항상 Ax = Bx 이면 A = B이다.
- C(BA) = (CB)A
- AB != BA
- (A+B)x = Ax + Bx
- AAA = \( A^3 \)
- \( (AB)^2 \neq A^2B^2 \)
## 역행렬
역행렬은 행렬 A의 역수이다. 표시는 \( A^{-1} \) 로 표시한다. 기본적으로 \( AA^{-1} = I \) 이다.
이 때 역행렬은 무조건 square matrix이다. square matrix가 아니면 역행렬이 존재할 수가 없다
### 성질
- \( (A^{-1})^{-1} = A \)
- \( (AB)^{-1} = B^{-1}A^{-1} \)
## 블록행렬
블록 행렬은 행렬 안에 행렬이 있는 것이다. 즉 행렬 안에 있는 행렬을 scalar 처럼 계산해서 도출하는 것이다.
직관적인 예시로는 다음의 식과 같다.
$$ A = \begin{pmatrix} A_1 & A_2 \\ A_3 & A_4 \end{pmatrix} $$
여기서 \( A_i \)는 각각의 행렬을 말한다. 이 때 행의 개수는 같아야한다. 즉 행렬 내에 수직선과 수평선을 그었을 때 끊기지 않고 1자로 쭉 연결되어야한다. 다음 사진은 블록 행렬의 예시이다

## 행렬을 이용한 여러 표현
### 고계 차분, 고계 미분
행렬을 이용한 방정식을 푸는 방법이다. 예를 들어 다음과 같은 식이 있다고 하자
$$ x_t = -0.7x_{t-1} - 0.5x_{t-2} + 0.2x_{t-3} + 0.1x_{t-4} $$
이러한 식을 해석하자면 오늘의 상태 \( x_t \)는 1,2,3,4 일 전의 상태에 의해 결정된다 라는 것이다. 이는 기초적인 시계열 식이다. 이를 vector 처럼 표현하면 \( x(t) = (x_t , x_{t-1},x_{t-2},x_{t-3})^T \) 로 나타난다. 이를 행렬로 표현해보자$$ x(t) = \begin{pmatrix} x_{t} \\ x_{t-1} \\ x_{t-2} \\ x_{t-3} \end{pmatrix} = \begin{pmatrix} -0.7 & -0.5 & 0.2 & 0.1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_{t-1} \\ x_{t-2} \\ x_{t-3} \\ x_{t-4} \end{pmatrix} $$
이 처럼 표현이 가능하다. 이러한 식을 다시 정리하면 \( x(t) = Ax(t-1) \) 의 형식을 띈다. 따라서 이를 이용하여 미분 형식에서도 동일하게 적용할 수 있다. t-1 을 \( d^{2}y(t)/dt \) 형식으로 나타내면서 미분방정식을 matrix를 이용하여 풀 수 있다.
## 좌표 변환
새로운 기저 백터에 대해 좌표를 계산하는 것을 좌표 변환(coordinate transform) 이라고 한다.
이는 예를 들어 설명하겠다.
두쌍의 기저를 사용하여 같은 벡터 v를 두 가지의 방식으로 표현해보면 다음과 같은 식이 도출되고 이를 정리하면 다음과 같다.

즉 이렇게 도출된 식이 \( v= (x,y)^T \) 에서 \( v' = (x',v')^T \)의 변환 규칙이다. 이렇게 변환 하는 과정을 좌표변환이라고 한다. 이 때 본질은 변하지 않음을 주의한다. 하나의 예를 들자면 한라산의 높이를 km로 나타내든 m로 나타내든 높이의 값은 동일하다는 것을 알아야된다.
이를 행렬로 표현하여 식을 표현하면 \( v = Av', v' = Av \) 처럼 된다. 즉, 이는 역행렬 관계를 갖게 된다.
위의 값을 예시로 행렬 표현을 해본다.
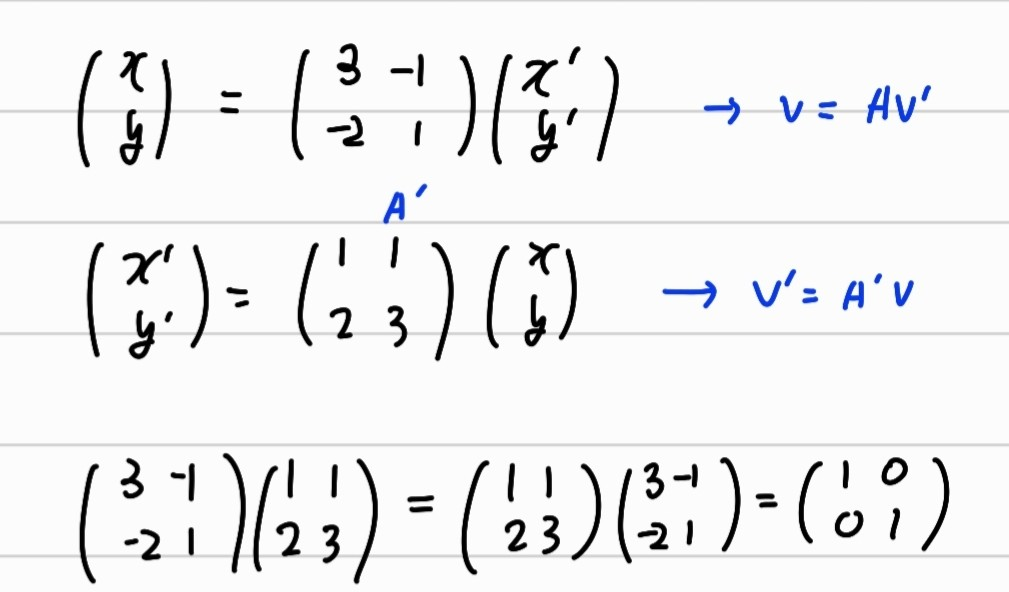
'Linear Algebra' 카테고리의 다른 글
| Rank 계산 (0) | 2022.01.02 |
|---|---|
| 차원 정리 및 Rank (0) | 2021.12.31 |
| 정칙행렬이 아닌 경우 (0) | 2021.12.28 |
| 정칙행렬의 연립방정식 풀이 (0) | 2021.12.26 |
| Vector,Matrix 기본(2) (0) | 2021.12.25 |




댓글