2021.12.24 - [Linear Algebra] - Vector, Matrix 기본(1)
Vector, Matrix 기본(1)
## Vector 벡터는 기본적으로 종벡터 형식으로 표현한다. ex) \( (1,2)^T \) 이러한 벡터로 이뤄진 것을 벡터공간(Vector space) 라고 한다. 벡터 공간을 나타내면 다음 사진과 같다. 벡터는 방향성 해석을
bigdata-analyst.tistory.com
## 전치 행렬(Transpose Matrix)
전치 행렬은 행렬 A에 대해 행과 열을 바꿔넣은 행렬을 전치 행렬이라고 한다.
예를 들면
$$ \begin{pmatrix} 2 & 9 & 4 \\ 7 & 5 & 3 \end{pmatrix} $$
의 전치 행렬은
$$ \begin{pmatrix} 2 & 7 \\ 9 & 5 \\ 4 & 3 \end{pmatrix} $$
이 된다.
그리고 이 전치행렬의 성질은 다음과 같다.
- \( (A^T)^T = A \)
- \( (AB)^{T} = B^{T}A^{T} \)
- \( (A^{-1})^{T} A^{T} = (AA^{-1} )^{T} = I^T = I \)
그리고 복소행렬에선 복소공역을 취하여 \( A^{*} \) 로 표현한다.
여기서 복소공역은 허수성분의 부호를 반전시킨 것이다.
## 확인(1)
Q : 만약 10차원 종벡터 \( x = (x_{1}, ... x_{10})^{T} \)에 대해 (v도 10차원 종벡터) \( y = xx^{T}(I+vv^{T})x \) 를 계산하여 shape을 말하시오.
이에 대한 풀이는 다음과 같다.
여기서 vector의 사이즈에 집중해보자. x = 10x1, x^T = 1x10 임을 알아야된다. 따라서 \( x^{T}x \)는 스칼라값이 나옴을 인지해야된다.

전개한 후 괄호를 적절하게 붙여서 스칼라값을 나오게 한 다음에 계산을 하면 훨씬 쉽게 풀이될 수 있다.
## 확인(2)
Q : 다음의 식을 증명하시오. \( c^{T}A^{-1}b \neq -1 \) , b,c는 n차 종벡터, A는 n차 square matrix

A:

양변에 좌항의 역행렬을 취한 값 즉 A+bc^T 를 곱해준다. 그러면 좌변은 항등행렬 I가 된다.
그리고 이를 전개하고, 이 과정에서 \( c^{T}A^{-1}b \) 는 스칼라값이므로 이를 이용하여 풀이를 이어나간다.
이 값을 괄호로 묶어준 후 \( A^{-1}bc^{T} \)로 묶어준다.
그 후 소거를 한 다음에 전개하면 I = I로 서로 같은 값이 나오게 된다.
## 행렬식
행렬식은 determinant 이라 하고 도형 관점에서 부피 확대율을 말한다.
행렬식은 det A 또는 \begin{vmatrix} A \end{vmatrix} 로 나타낸다.
여기서 determinant는 확대율 이기 떄문에 음수도 나올 수 있다는 점에 유의한다.
행렬식을 부피 확대율로 해석할 때 다중적분의 변수 변환에서 매우 중요한 역할을 한다. 이 때 이용되는 것이 jacobian matrix이다. jacobian matrix에 대해선 추후에 다시 설명하겠다.
행렬식의 성질은 다음과 같다.
- \( \det I = 1 \)
- \( \det(AB) = \det(A) \det(B) \)
- \( \det A^{-1} = \frac{1}{\det A} \)
- \( \det A = 0 \) 이면 \( A^{-1} \) 은 존재하지 않는다.
- 행렬의 두 열이 완전히 같은 경우는 \( \det A = 0 \) 이다.
- \( \det(A^{T}) = \det A
- \( det(cA) = c^{n} det A \)
- 어느 열의 정수배를 다른 열에 더해도 값이 변하지 않는다.
마지막 성질에 대해서 덧붙이면 다음과 같은 예시로 설명 한다.
\begin{pmatrix} 1 & 1 & 5 \\ 1 & 2 & 7 \\ 1 & 3 & 6 \end{pmatrix} \begin{pmatrix} 1 & 1 & 5 \\ 1 & 2 & 7 \\ 15 & 27 & 36 \end{pmatrix}
이와 같은 두 행렬이 있을 때 두 행렬의 행렬식은 서로 같다. 첫번째 행렬을 A라고 하고, 두번째 행렬을 B라고 하자. 여기서 \( B_{:,3} = A_{:,3} + 10A{:,2} \) 를 적용해도 행렬식이 같게 나온다.
이를 python 코드로 구현하면 다음과 같다.
import numpy as np
A = np.array([[1,1,5],[1,2,7],[1,3,6]])
B = np.array([[1,1,15],[1,2,27],[1,3,36]])
print(np.linalg.det(A)) # -3
print(np.linalg.det(A)) # -3numpy의 linalg 모듈을 이용하여 계산한다.
이러한 성질은 벡터의 성질을 생각하면 이해하기 쉽다. 즉, 3차원 도형에서 방향을 밀어도 부피는 변하지 않는다는 점이다. 즉 A의 3번째 컬럼을 2번째 컬럼 방향으로 밀어도 단순히 방향이 바뀐 것이지 길이가 바뀐 것이 않기 떄문에 부피는 동일하다.
이러한 행렬식은 상삼각행렬 (upper traingular matrix) 이면 determinant의 계산은 쉬워진다.
상삼각행렬은 다음과 같다.

여기서 빈 부분은 모두 0의 값을 가진다고 생각하면 된다. 이러한 행렬에서 determinant를 계산하면 대각성분의 곱으로 나타낼 수 있다. 즉, 위 그림이 3x3 matrix라고 할 때 det U = u11*u22*u33 이 되는 것이다.
이러한 형태의 행렬은 평행육면체가 되고 , a11*a22는 밑변 X 높이의 값이된다. 그리고 거기에 높이 값 a33을 곱해줘서 평행육면체의 부피 = 상삼각행렬의 행렬식이 된다.
## 행렬식 계산 방법(Laplace 전개)
먼저 간단하게 2x2 matrix에서 행렬식을 알아보자.
사실 이건 고등학교때 배운것이므로 매우 간단하고 기억이 안나더라도 이 식을 보면 바로 기억날 것이다.
det A = ad - bc
바로 기억할 것이다. 역행렬에서도 분모가 되는 스칼라값이기 때문에 다들 기억할 것이다.
따라서 이를 기반으로 계산하는 행렬식에 대해 알아보자.
먼저 3x3 matrix를 기반으로 계산을 해보자
지금부터 계산하는 방식은 여인수 전개(Laplace 전개)의 방식으로 전개하는 것이다.
일단 일반적인 식부터 살펴보면 다음과 같다.
$$ \det A = a_{1j} \Delta_{1j} + ... + a_{nj} \Delta_{nj} $$
이 식을 보면 감이 안올것이다. 예시 변수를 들어서 한 번 해보자
다음과 같이 3x3 matrix일 때 구성은 이렇게 된다.

여기서 -1에 지수 값을 정해지는 것은 기준으로 잡는 값의 위치이다. 처음은 \( a_{11} \) 로 잡았기 때문에 지수 값은 1+1로 2가 된다. 또한 여기서 기준을 잡은 행과 열을 제외한 나머지 행렬을 이용하여 행렬식을 계산하면 행렬식이 계산된다.
하나의 예시를 들어서 풀어보자
앞에서 사용했던 행렬을 이용하여 행렬식 계산을 손으로 해보자
\begin{pmatrix} 1 & 1 & 5 \\ 1 & 2 & 7 \\ 1 & 3 & 6 \end{pmatrix}

1행을 기준으로 풀이를 한 것이다.
따라서 1행의 값들을 기준으로 곱해주고 1행 1열, 1행 2열 순으로 계산할 때 제외하며 값을 계산한다.
이러한 Laplace 전개를 통해서 행렬식 뿐만 아니라 역행렬도 구할 수 있다.
이는 여인수 행렬(adjugate matrix)를 통해서 구할 수 있다.
사실 여인수 행렬은 이미 행렬식을 구할 때 살펴보았다.
행렬식을 계산할 때의 소행렬을 여인수라고 한다. 이를 식으로 한 번 나타내면 다음과 같다. 행렬 A가 다음과 같이 존재할 때
\begin{equation*}
A_{m,n} =
\begin{pmatrix}
a_{1,1} & a_{1,2} & a_{1,3} \\
a_{2,1} & a_{2,2} & a_{2,3} \\
a_{3,1} & a_{3,2} & a_{3,3}
\end{pmatrix}
\end{equation*}
1행 1열의 여인수 \( C_{11} \) 는 \( (-1)^{1+1} (a_{22}a_{33} - a_{23}a){32}) \) 이다.
따라서 이를 일반화 하여 \( C \)로 나타내는데 식은 다음과 같다.
$$ C_{ij} = (-1)^{i+j}M_{ij} $$
여기서 \( M_{ij} \)는 소행렬 식이다.
이러한 여인자 행렬을 기반으로 수반행렬(adjoint matrix)를 구할 수 있는데 이는 여인자 행렬에 Transpose를 취해준 것이다.
\begin{equation*}
adj \, A =
\begin{pmatrix}
C_{1,1} & C_{1,2} & \cdots & C_{1,n} \\
C_{2,1} & C_{2,2} & \cdots & C_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
C_{m,1} & C_{m,2} & \cdots & C_{m,n}
\end{pmatrix}^{T}
\end{equation*}
이를 이용하여 역행렬은 다음의 식과 같이 정의된다.
$$ A^{-1} = \frac{1}{\det A}adj \, A $$
마지막으로 이 방법을 직접적인 숫자의 대입을 통해 봐보자

이러한 역행렬을 파이썬 코드로 확인해보자

여인자 행렬을 이용한 역행렬을 구하는 과정과 실제 python code상의 역행렬과의 값을 비교해봤을 때 동일함을 알 수 있다.
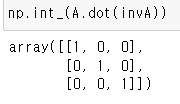
당연한 말이지만 A와 invA의 행렬곱을 통해서도 I의 값이 나오는 것을 알 수 있다.
'Linear Algebra' 카테고리의 다른 글
| Rank 계산 (0) | 2022.01.02 |
|---|---|
| 차원 정리 및 Rank (0) | 2021.12.31 |
| 정칙행렬이 아닌 경우 (0) | 2021.12.28 |
| 정칙행렬의 연립방정식 풀이 (0) | 2021.12.26 |
| Vector, Matrix 기본(1) (0) | 2021.12.24 |




댓글