대각화할 수 없는 경우

그 전까지 포스팅에선 대각화 가능한 경우에서의 real time 즉, continuos 한 time 이 진행될 때의 미분방정식 풀이를 통하여 행렬 A에 대한 수렴과 발산 여부를 알아보았다.

2022.02.08 - [Linear Algebra] - Real Time system

Real Time system

 

하지만 대각화가 불가능한 경우에 대해선 알아보지 못하였다. 따라서 이번 포스팅에서는 대각화가 불가능한 경우에 대해서 어떻게 수렴과 발산 판정을 하는지에 대해 알아보겠다.

먼저 결론부터 말하면 대각화 가능한 경우와 거의 유사하다.

$x(t)=Ax(t-1)$ 이라는 discrete한 시간이 있을 때 다음과 같은 성질을 만족한다.

• A의 eigenvalue $\lambda$ 에서 $|\lambda |>1$ 인 것이 하나라도 있으면 발산한다.
• 모든 eigenvalue $\lambda$가  $|\lambda |<1$ 이면 발산하지 않는다.
• 모든 eigenvalue $\lambda$ 가 $|\lambda |\le 1$ 이지만 $|\lambda |=1$ 이면 eigenvalue 만으로 발산과 수렴을 판단할 수 없다.

$\frac{d}{dt}x(t)=Ax(t)$ 이라는 continuous한 시간이 있을 때 다음과 같은 성질을 만족한다.

• A의 모든 eigenvalue $\lambda$에 $\lambda >0$인 것이 하나라도 있으면 발산한다
• 모든 eigenvalue $\lambda$가 $\lambda <0$ 이면 발산하지 않는다(수렴)
• 모든 eigenvalue $\lambda \le 0$ 이지만 $\lambda =0$ 이면 eigenvalue만으로는 판정할 수 없다.

 

이제 이와 같은 결론을 도출하는 과정을 봐보자

 

## Jordan Normal Form(요르단 표준형)

대각화 할 수 없는 square matrix A에 대해서 대각에 가까운 jordan form이면 변환할 수 있다. 즉, $P^{-1}AP=J$가 jordan 표준형이 될 수 있도록 만드는 것이다.

jordan 표준형은 다음과 같은 형태를 따른다.

jordan normal form

즉, 블록대각형태를 띄는 형태이다. 그 중 대각블록은 대각성분에 같은 수가 나열 되고, 그 위의 오른쪽 위는 1이 대각값을 가진다. 이러한 블록을 jordan cell 이라고 한다. 위 예시에선 크기가 3인 jordan cell, 1 인 jordan cell, 2 인 jordan cell 이 2개 를 가진 형태이다.

여기서 좀 더 예시를 봐보자. 프로그래머를 위한 선형대수학에 있는 예시이다.

여기서 Jordan matrix가 아닌 것을 찾아보자.

 

 

정답은 J2와 J3 이다.

맞는 것들을 한 번 봐보자. 이는 블록으로 잘 나눠지는가를 판단하면 된다.

다음과 같이 블록을 나눌 수 있음을 보인다.

그럼 이제 jordan matrix의 성질을 알아보자

### jordan matrix의 eigenvalue

하나의 jordan matrix로 살펴보자

$$B=\left(\begin{array}{cccc}7& 1& 0& 0\\ 0& 7& 1& 0\\ 0& 0& 7& 1\\ 0& 0& 0& 7\end{array}\right)$$

위 matrix B에선 eigen value는 7밖에 없다. 그리고 eigenvector는 $p=(a,0,0,0{)}^T$ 이다. 

그렇다면 위에서 Jordan form에 대한 예시를 들었던 행렬 J에 대해서는 eigenvalue가 어떨까

간단하게 알아보면 block의 대각값이라는 것을 알 수 있다. 

즉 J의 eigenvalue는 2(4중),3(2중),0(2중) 이 된다. 하지만 여기서 0이 아닌 다른 임의의 수 1로 하자. (0일 떈 경우가 다름).

 그럼 여기서의 eigenvector값은 eigenvalue가 2일 때 $\alpha ,0,0,0,0,0,0,0{)}^T$ 가 되고 eigenvalue가 3일 때 $0,0,0,0,\beta ,0,0,0{)}^T$, eigenvalue가 1일 떈 $0,0,0,0,0,0,\gamma ,0{)}^T$ 가 된다. 물론 여기서 언급한 $\alpha ,\beta ,\gamma$ 는 0이 아니다.

 

결국 위와 같은 것을 정리하면 jordan matrix J의 성질은 다음과 같다.

• 대각 성분이 eigenvalue $\lambda$ 이다.
• 대각성분 eigenvalue $\lambda$ 개수가 eigenvalue $\lambda$가 몇 중해인지(대수적 중복도(algebraic multiplicity))에 대응
• 대각성분이 $\lambda$인 jordan cell 개수가 eigenvalue $\lambda$에 linear independent 한 eigen vector의 개수(기하적 중복도(geometric multiplicity))에 대응

따라서 square matrix A가 jordan matrix로 변환되면 A의 eigenvalue와 eigenvector가 어떻게 구성 되어있는지 알 수 있따. 특히 eigen value에 중복해가 없을 경우 대각행렬이 될 수 밖에 없다.

 

## Jordan matrix의 거듭제곱

Jordan matrix의 거듭제곱의 계산은 평범하게 해도 되지만 분해해서 진행을 하면 좀 더 편하다.

square matrix B는 앞서 예시를 든 그 matrix를 사용한다.

$$B=\left(\begin{array}{cccc}7& 1& 0& 0\\ 0& 7& 1& 0\\ 0& 0& 7& 1\\ 0& 0& 0& 7\end{array}\right)$$

여기서 $B=7I+Z$ 로 분해할 수 있다. 여기서 Z는 다음과 같다.

$$Z=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right)$$

이 Z 는 왼쪽에 곱해지냐 오른쪽에 곱해지냐에 따라 어떻게 행렬이 변화할지 예측이 가능하다.

만약에 Z가 왼쪽에 곱해지면 1행이 밀리는 효과( 예시 1 참고) , 오른쪽에 곱해지면 1열이 밀리는 효과(예시 2 참고) 를 가진다.

- 예시 1

$$\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right)\left(\begin{array}{c}a\\ b\\ c\\ d\end{array}\right)=\left(\begin{array}{c}b\\ c\\ d\\ 0\end{array}\right)$$

- 예시 2

$$\left(\begin{array}{cccc}a& a_1& a_2& a_3\\ b& b_1& b_2& b_3\\ c& c_1& c_2& c_3\\ d& d_1& d_2& d_3\end{array}\right)\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right)=\left(\begin{array}{cccc}0& a& a_1& a_2\\ 0& b& b_1& b_2\\ 0& c& c_1& c_2\\ 0& d& d_1& d_2\end{array}\right)$$

이 행렬을 이미지라고 생각하면 행이 밀리는 것은 이미지가 위로 올라가는 효과, 열이 밀리는 것은 이미지가 옆으로 밀리는 효과를 의미한다.

이러한 성질을 사용하면 Z를 거듭제곱할 떄 마다 옆으로 몇칸 더 밀리고 결국 많이 밀면 O 행렬을 갖는다는 것을 알 수 있다. 

따라서 $B^2$ 을 계산할 때 , $B^2=(7I+Z{)}^2=7^{2}I+2\cdot 7Z+Z^2$ 이고 이를 계산하면

$$B^2=\left(\begin{array}{cccc}{7}^2& 2\cdot 7& 1& 0\\ 0& 7^2& 2\cdot 7& 1\\ 0& 0& 7^2& 2\cdot 7\\ 0& 0& 0& 7^2\end{array}\right)$$

이런식으로 값이 계산된다. 그러면 더 나아가서 $B^3$ 일 때는 다음과 같이 나온다.

$$B^3=\left(\begin{array}{cccc}{7}^3& 3\cdot 7^2& 3\cdot 7& 1\\ 0& 7^3& 3\cdot 7^2& 3\cdot 7\\ 0& 0& 7^3& 3\cdot 7^2\\ 0& 0& 0& 7^3\end{array}\right)$$

다음은 4일 떄이다.

$$B^4=\left(\begin{array}{cccc}{7}^4& 4\cdot 7^3& 6\cdot 7^2& 4\cdot 7\\ 0& 7^4& 4\cdot 7^3& 6\cdot 7^2\\ 0& 0& 7^4& 4\cdot 7^3\\ 0& 0& 0& 7^4\end{array}\right)$$

이러한 특징을 보다보면 결국 하나의 규칙이 나오게 되는데 , 따라서 일반항은 다음과 같다.

$$B^t=\left(\begin{array}{cccc}{7}^t& t\cdot 7^t& {}_t{C}_2& {}_t{C}_3\cdot 7^{t-3}\\ 0& 7^t& t\cdot 7^t& {}_t{C}_2\\ 0& 0& 7^t& t\cdot 7^t\\ 0& 0& 0& 7^t\end{array}\right)$$

이렇듯 대각 성분이 $\lambda$ 인 jordan cell B에 대해 B^{t} 를 계산하면 ${}_t{C}_s{\lambda }^{t-s}$ 항이 나타난다. 이렇게 해서 더욱 일반화 된 식을 봐보자

$f^{(s)}(\lambda )=\frac{d^s}{d{\lambda }^s}f(\lambda )$ 로 나오는데 이는 $f(\lambda )={\lambda }^t$ 로 두고 , $f$ 를 $\lambda$로 s 회 미분한 식이다. 

그러면 m 크기의 jordan 셀 B는 다음과 같이 이뤄진다.

그러면 이 jordan cell의 t 제곱은 다음과 같이 형성이 된다.

$B^t$

 

이와 같이 특정한 패턴을 가지면서 구성됨을 알 수 있다. (예시와 동일) 

여기서 $\frac{1}{s!}{f}^{(s)}(\lambda )$ 는 taylor 전개의 각 항과 같고 이는 ${}_t{C}_s{\lambda }^{t-s}$ 와 같다.

---

※ Taylor 전개 

$$f(x)=f(\lambda )+f^{(1)}(\lambda )(x-\lambda )+\frac{1}{2!}{f}^{(2)}(\lambda )(x-\lambda {)}^2+\frac{1}{3!}{f}^{(3)}(\lambda )(x-\lambda {)}^3+\cdots$$

---

이러한 성질을 이용하면 문제가 쉽게 풀릴 수 있다. 예를 들어 $C=3B^7-2B^5+8I$ 와 같은 다항식을 $f(\lambda )=3{\lambda }^7-2{\lambda }^5+8$로 두면 C는 위 예시와 같은 꼴( $B^t$ 이 나온다.

그러면 결국 저 꼴을 이용하여 계산을 하면 되므로 간단해진다.

여기서 핵심은  3 (${\lambda }^7)의미분)-2(\text{(}{\lambda }^5)의미분)+8(1의미분)=\text{(}3{\lambda }^7-2{\lambda }^5+8$ 라는 점이다. 

이런 jordan cell B를 이용하여 전체 jordan matrix의 거듭제곱 계산을 해보자. 다음과 같은 J matrix가 있다고 하자

jordan matrix

 

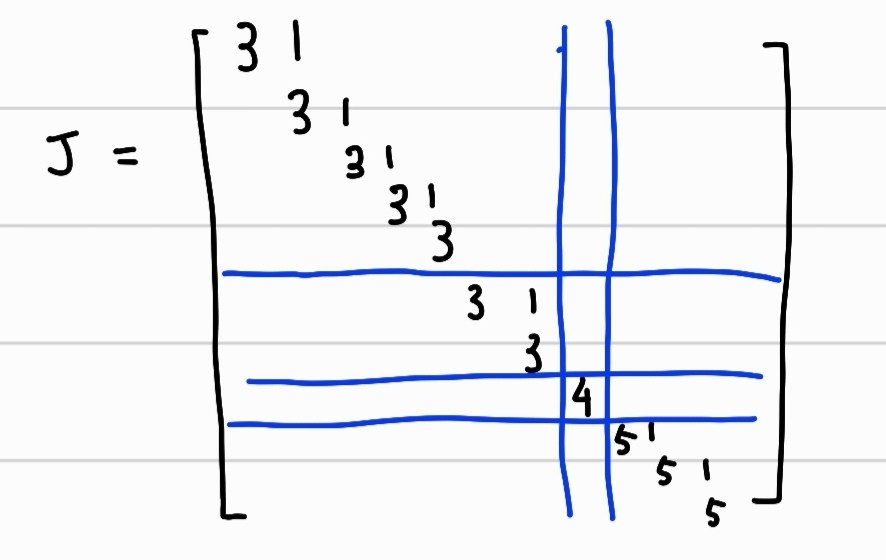
여기서 각각의 jordan cell은 다음과 같다.

jordan cell list

이런 jordan matrix에서 t 제곱을 하면 각각의 jordan cell에 t제곱한 것을 결합한 형태가 완성된다.

jordan matrix t제곱

 

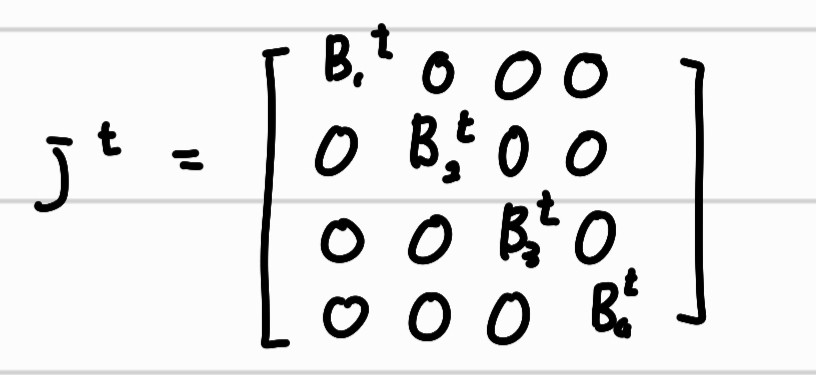
이러한 결론을 바탕으로 jordan standard form이 아닌 matrix도 jordan form으로 만들면 모두 거듭제곱을 계산할 수 있게된다.

따라서 $P^{-1}AP=J$는 $PJ{P}^{-1}=A$이고 이를 통해 거듭제곱을 하면 $A^t=(PJ{P}^{-1}{)}^t=P{J}^t{P}^{-1}$가 형태로 되서 계산할 수 있게 된다.