이 장에 앞서 데이터셋을 다운 받아야한다. MNIST라는 데이터 셋을 다운 받는다.
이 데이터셋은 sklearn 모듈에 포함 되어 있으므로 이를 다운 받으면 된다.
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784',version=1)
mnist위 데이터 셋은 7만개의 행과 784개의 열로 이루어져 있다. 각 열은 pixel 하나의 값이므로 한 글자의 크기가 28x28 로 이루어져있다.
이 중 하나의 숫자를 시각화 해보면 다음과 같다.
import matplotlib
some_digit=X[36000]
some_digit_image = some_digit.reshape(28,28)
some_digit_image
plt.imshow(some_digit_image,cmap='binary')
plt.axis('off')
plt.show()
숫자 9이다.
MNIST 데이터셋은 이미 trian set과 test set이 나누어져 있다. 60000을 기준으로 그 전은 train, 다음은 test이다.
train과 test를 분리하자
X_train,y_train,X_test,y_test = X[:60000],y[:60000],X[60000:],y[60000:]그리고 랜덤으로 섞어준다. 데이터의 순서가 영향을 줄 수 있는 경우도 있기 때문이다.
import numpy as np
shuffle_index = np.random.permutation(60000)
X_train,y_train = X_train[shuffle_index],y_train[shuffle_index]numpy random에 permutation 함수를 통해 60000개를 무작위의 순서로 섞는다.
이렇게 나눈 데이터셋을 가볍게 SGDClassifier 모델을 통해 분류해본다.
SGD는 확률적 경사하강법 분류기인데 이 분류기는 매우 큰 데이터셋을 효율적으로 처리한다. SGD는 한 번에 하나씩 훈련 샘플을 독립적으로 처리하기 때문이다. 이에 대한 자세한 내용은 추후에 다루도록 하겠다.
이진분류를 위해 9인 것과 9가 아닌 것이라고 한 후 이를 분리한다.
y_train_9 = (y_train == '9')
y_test_9 = (y_test == '9')이제 훈련 시킨다.
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(max_iter = 5,random_state=42)
sgd_clf.fit(X_train,y_train_9)이 훈련된 모델로 숫자 9의 이미지를 감지한다.
sgd_clf.predict([some_digit])
'''
array([False],dtype=bool)
'''흠...틀렸다! 하지만 하나 틀렸다해서 이 분류기를 나쁜 분류기라고 특정 지을 순 없다. 좋은 분류기 나쁜 분류기를 특정짓기 위해선 성능을 측정해야되는데 성능 측정 방법에 대해 더 자세히 알아보겠다.
## 교차검증을 위한 정확도 측정
교차 검증은 그 전 장에서도 다뤘든 많이 쓰는 방법이다. 전 장에서는 train set 과 test set을 계층 추출을 하였다면 이번에는 validation set도 한 번 계층적으로 sampling 하여 평가해본다.
# 교차 검증
from sklearn.model_selection import StratifiedKFold,cross_val_score
cross_val_score(sgd_clf,X_train,y_train_9,cv=3,scoring='accuracy')StratifiedKFold 모듈을 통해 3번 검정용 데이터셋을 계층 추출하여 비교한다. 이를 cross_val_score를 통해 교차 검증을 수행한다. 이번의 평가 척도는 accuracy 정확도로 점수를 매긴다.
이 결과 array([0.9453 , 0.94385, 0.91885]) 로 약 90퍼센트의 정확도로 9인 것을 맞춘다.
이와 반대로 9가 아닌 것을 한 번 교차검증을 수행해보자
from sklearn.base import BaseEstimator
class Never9Classifier(BaseEstimator):
def fit(self,X,y=None):
pass
def predict(self,X):
return np.zeros((len(X),1),dtype=bool)
never_9_clf = Never9Classifier()
cross_val_score(never_9_clf,X_train,y_train_9,cv=3,scoring='accuracy')
이 결과 array([0.90135, 0.89935, 0.90185]) 로 약 90퍼센트의 정확도가 측정된다. 비록 아까의 숫자 하난 못맞췄지만 다른 것에 대해선 약 90퍼센트의 정확도로 꽤 잘 맞추는 분류기임을 알 수 있다.
## 오차 행렬(confusion matrix)
단순하게 맞췄다 안맞췄다라는 정확도가 아닌 잘못 맞춘 횟수 등을 알고 싶다면 오차 행렬을 사용해야된다.
이를 측정하기 위해 검정용 데이터 셋에서 예측값을 뽑아내보자
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf,X_train,y_train_9,cv=3)cross_val_predict 모듈을 사용하면 점수가 아닌 예측값을 반환해준다.
그리고 sklearn.metrics의 confusion_matrix의 모듈을 사용하여 오차 행렬을 추출한다.
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_9,y_train_pred) # true_y,pred_y
'''
array([[52878, 1173],
[ 2667, 3282]], dtype=int64)
'''어떠한 행렬이 반환되었다. 이 행렬은 개수를 나타내는데 이에 대해서 더 세부적으로 알아보자
이 행렬을 표로 그리면 다음과 같다.

이 각각의 의미를 설명하자면
TN(True Negative) : 진짜 음성으로 9가 아닌 것을 아니다라고 정확하게 분류한 개수이다.
FP(False Positive) : 가짜 양성으로 9가 아닌 것을 9라고 분류한 개수이다.
FN(False Negative) : 가짜 음성으로 9인 것을 9가 아니라고 분류한 개수이다.
TP(True Positive) : 진짜 양성으로 9인 것을 9라고 정확하게 분류한 개수이다.이러한 숫자의 개수를 하나의 점수(비율)로 나타내는 지표가 있다.바로 정밀도(Precision)와 재현율(Recall)이다.

Precision을 풀어서 표현하면 -> 양성이라고 판단한 것 중에 진짜 양성인 것
Recall or Sensitivity를 풀어서 표현하면 -> 실제 양성이라고 하는 것들 중에 진짜 양성인 것
Recall은 진짜 양성 비율(TPR) 라고 불리우고 민감도(sensitivity)라고 불린다
이러한 정밀도와 재현율을 하나의 점수로 표현하려면 어떻게 해야할까? 이는 F1-score로 표현된다.
## F1 score
F1-score란 정밀도와 재현율의 조화 평균이다.
from sklearn.metrics import precision_score,recall_score
precision_score(y_train_9,y_train_pred) # 정밀도
# 0.7367003367003367
recall_score(y_train_9,y_train_pred) # 재현율
# 0.5516893595562279
from sklearn.metrics import f1_score
f1_score(y_train_9,y_train_pred) # f1 score
# 0.6309111880046135
위와 같은 식 때문에 정밀도와 재현율은 항상 Trade Off 관계가 된다.
확률적 경사하강법을 통해 이러한 Trade Off 관계를 이해해보자.
SGD는 결정 함수(Decision function)을 통하여 각 샘플의 점수를 계산한다. 따라서 임계값에 따라 맞다 틀리다가 나눠진다고 생각하면 된다.
적정선의 임의의 임계값이 0이라고 할 때 임계값을 5만큼 높힐 때 정밀도는 높아진다. 하지만 이 때 재현율은 낮아진다.
만약 5만큼 감소를 시키면 이와 반대로 재현율이 높아지고 정밀도는 낮아진다.
따라서 이러한 임계값을 최적화 시키는 것이 중요하다. 이를 위해 정밀도와 재현율의 그래프를 한 번 그려보자
from sklearn.metrics import precision_recall_curve
precisions,recalls,thresholds = precision_recall_curve(y_train_9,y_scores)
def plot_precision_recall_vs_threshold(precisions,recalls,thresholds):
plt.plot(thresholds,precisions[:-1],"b--",label='precision')
plt.plot(thresholds,recalls[:-1],'g-',label='recall')
plt.xlabel('threshold')
plt.legend(loc='center left')
plt.ylim([0,1])
plot_precision_recall_vs_threshold(precisions,recalls,thresholds)
plt.show()
sklearn의 precision_recall_curve를 통해 정밀도와 재현율 임계값을 계산한 후 이를 plot으로 그린 것이다.
위 그래프를 보았을 때 적정이 임계치는 0에 조금 더 가까운 -50만과 0 사이 임을 알 수 있다. 대략 -2만 정도로 추측된다.
그래프를 보다보니 조금 울퉁불퉁한 부분이 있다. 이는 임계치를 올리더라도 정밀도가 가끔 낮아질 때가 있기 때문이다.(일반적으로는 높아져야한다.) 하지만 재현율은 임계값이 올라감에 따라 줄어들 수 밖에 없기 때문에 부드러운 곡선이 나온다.
## ROC curve
ROC curve는 이진 분류에서 널리 사용하는 도구이다. 이는 precision & recall curve와 비슷하지만 거짓 양성 비율(FPR)에 대한 진짜 양성 비율(TPR)이다.
앞서 언급했듯이 TPR은 Recall과 같다. 그렇다면 FPR은 무엇일까?

FPR은 양성으로 잘못 분류된 음성 샘플의 비율이다. 이는 1에서 음성으로 정확하게 분류한 음성 샘플의 비율(TNR)을 뺀 것이다. TNR은 특이도(specificity)라고 불리운다. 따라서 ROC curve는 민감도에 대한 1-특이도 그래프 라고 불리운다.
from sklearn.metrics import roc_curve
fpr,tpr,thresholds = roc_curve(y_train_9,y_scores)
def plot_roc_curve(fpr,tpr,label=None):
plt.plot(fpr,tpr,linewidth=2,label=label)
plt.plot([0,1],[0,1],'k--')
plt.axis([0,1,0,1])
plt.xlabel('FPR')
plt.ylabel('TPR')
plot_roc_curve(fpr,tpr)
plt.show()sklearn.metrics 의 roc_curve 모듈을 통해 fpr과 tpr을 계산한 후 이에 대해 그래프를 그린다.
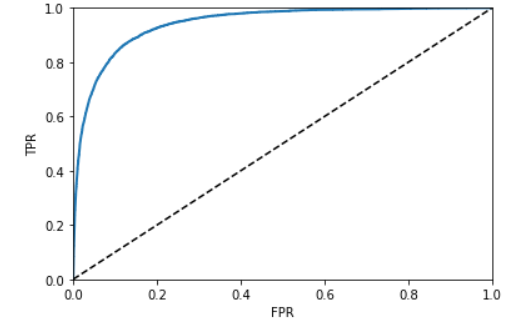
roc 커브가 볼록할 수록 더 좋은 분류기를 뜻한다. 이 볼록도를 측정하는 것을 AUC 라고 한다.
AUC는 곡선 아래의 면적이다.

이를 계산하기 위해선
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_9,y_scores)
# 0.9424104816939807위와 같은 모듈을 통해 계산할 수 있다.
SGDClassifier는 0.94의 AUC가 나왔다. 그럼 다른 분류기는 어떠할까?
대표적인 앙상블 모델인 RandomForestClassifier로 비교해보자
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state = 42)
y_probas_forest = cross_val_predict(forest_clf,X_train,y_train_9,cv=3,method='predict_proba')RandomForest는 SGD와 다르게 decision_function() 메서드가 없다. 하지만 predict_proba() 메서드가 있다.
이 method는 샘플이 행, 클래스가 열이고 주어진 클래스에 속할 확률을 담은 배열을 반환한다.
ROC curve를 그리려면 확률이 아니라 점수가 필요한데 이를 위해서 양성 클래스에 대한 확률을 사용한다.
y_scores_forest = y_probas_forest[:,1] # 양성 클래스에 대한 확률
fpr_forest,tpr_forest,thresholds_forest = roc_curve(y_train_5,y_scores_forest)
plt.plot(fpr,tpr,'b:',label='SGD')
plot_roc_curve(fpr_forest,tpr_forest,'RandomForest')
plt.legend(loc='lower right')
plt.show()
SGD보다 더 좋음을 알 수 있다! AUC를 알아보자
roc_auc_score(y_train_9,y_scores_forest)
# 0.9952284858725549무려 0.99라는 점수가 나온다.
'핸즈온 머신러닝' 카테고리의 다른 글
| Chapter 4 - 모델 훈련(1) (0) | 2021.01.31 |
|---|---|
| Chapter2 - 머신러닝 프로젝트 처음부터 끝까지(3) (0) | 2021.01.05 |
| Chapter2 - 머신러닝 프로젝트 처음부터 끝까지(2) (0) | 2021.01.05 |
| Chapter2 - 머신러닝 프로젝트 처음부터 끝까지(1) (1) | 2021.01.04 |
| Chapter1 - 한눈에 보는 머신러닝 (1) | 2020.12.29 |




댓글