## 1. 선형회귀

선형회귀는 입력 특성의 가중치 합과 편향(theta0)라는 상수를 더해 예측을 만드는 것이다. 다음과 같이 벡터 형식으로도 나타낼 수 있다.

행렬곱을 이뤄내기 위해 theta에 전치를 한다.
이러한 선형 모델의 비용함수는 어떤 것이 있는지 살펴보자. 앞서 회귀에서 MSE의 지표를 다뤘다. 이 MSE함수를 다시 언급한다.

이러한 평균오차제곱(MSE)를 최소화 하는 것이 모델 훈련의 목표이다.
- 정규방정식 : 비용 함수(여기서는 MSE)를 최소화하는 theta 값을 찾아주는 방법을 정규방정식이라고 한다.

이 정규 방정식을 테스트하기 위해서 y = 4+3x + noise라는 식을 생성한다.
X = 2*np.random.rand(100,1)
y = 4+3*X+np.random.randn(100,1)
다음과 같이 생성이 되었다. 정규 방정식을 사용해 다음 식의 theta를 예측해본다. 이 때 유사 역행렬을 구하는 numpy의 inv() 함수를 통해서 계산을 한다.
X_b = np.c_[np.ones((100,1)),X] # 모든 샘플에 X0=1 추가
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) # 정규 방정식
theta_best
'''
array([[3.75303695],
[3.08571225]])
'''다른 사람들이 직접 실행해보면 radom의 노이즈 때문에 값이 달라진다.
예측 결과 theta0 = 4, theta1=3의 정확한 값을 기대했지만 유사하긴 하지만 엄청 정확하다라고는 할 수 가 없다. 이는 노이즈때문에 발생하는 현상이다.
다음으로 앞서 예측한 theta hat(theta0,theta1)을 통해 예측을 해본다.
X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)),X_new]
y_predict = X_new_b.dot(theta_best)
y_predict
'''
array([[3.75303695],
[9.92446145]])
'''
직관적으로 판단하기 위해 그래프를 그려본다.

꽤 잘 나왔음을 알 수 있다! 위와 같은 정규 방정식을 통해 선형 회귀 예측이 가능하다는 것을 보여준다.
이를 sklearn으로 구현하면 다음과 같다.
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
lin_reg.intercept_,lin_reg.coef_ # (array([3.75303695]), array([[3.08571225]]))
lin_reg.predict(X_new)
'''
array([[3.75303695],
[9.92446145]])
'''
## 경사하강법
경사하강법(Gradient Descent)의 기본 아이디어는 비용 함수를 최소화 하기 위해 반복해서 파라미터를 조정해나가는 것이다. 직관적인 그림으로 설명하겠다.
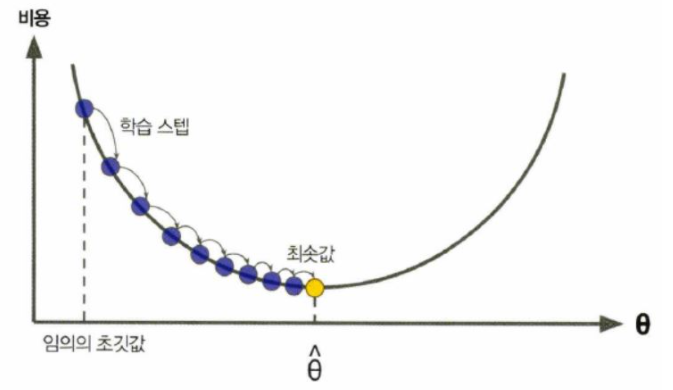
최소의 Gradient(기울기)로 도달하기 위해 반복해서 파라미터를 조절하는 방법이다.
그림에서 최솟값 theta hat을 찾기 위해 step만큼을 내려간다. 이를 learning rate 라고 부르며 가장 중요한 파라미터이다. 너무 크게크게 내려가면 최솟값을 못찾을 수도 있고, 너무 조금씩 내려가면 많은 반복을 통해 내려가야 되기 때문에 적절한 학습 step을 찾는 것이 가장 중요하다.
여기서 경사하강법의 문제가 발생한다. 현실의 데이터는 저렇게 깔끔하게 2차 함수의 형태로 존재하지 않는다는 것이다.

밑으로 내려가다보면 전체 그래프에서 최소값이 아닌 지역 최솟값에 빠져서 0으로 수렴하게 된다. 또한 오른쪽에서 시작한다면 평탄한 지역을 지나기 위해 시간이 오래걸리고 일찍 멈추어 전역 최솟값에 도달하지 못한다.
하지만 다행히 MSE 비용함수는 볼록함수로써 연속된 값이고 지역 최솟값이 존재하지 않는다. 그리고 기울기가 급작스럽게 변하는 일이 없기 때문에 결국엔 전역 최솟값으로 수렴이 가능하다.
※ 이 때 모든 특성들이 같은 스케일을 가지고 있어야한다.(ex. StandardScale, MinMaxScale)
그렇지 않으면 최솟값으로 수렴하는데 시간이 오래 걸린다.

## 배치 경사하강법
경사하강법을 구현하려면 각 모델 파라미터 세타에 대해 비용 함수의 그래디언트를 계산해야한다. 즉, 세타가 조금 변경될 때 비용 함수가 얼마나 바뀌는 지 계산해야한다. 이를 편도함수라 한다.
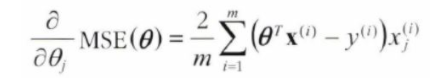
위 식은 MSE의 식에서 세타를 편미분한 것이다. 이를 전체 데이터에 대해서 MSE의 편도함수를 계산한다면 다음과 같다.

이러한 공식은 배치 경사하강법이라고 한다. 배치(묶음)를 주어 훈련을 빠르게 이뤄낸다.

에타(learning rate)가 음수인 이유는 위로 향하는 그라디언트 벡터가 구해지면 반대 방향인 아래로 가야되기 때문이다.
에타는 앞서 말했듯이 경사하강법의 스텝의 크기이다. MSE의 편도 함수에 스텝의 크기를 가중치로 주어 다음 theta 값(파라미터 값)을 정한다.
eta = 0.1
n_iterations = 1000
m = 100
theta = np.random.randn(2,1)
for iteration in range(n_iterations):
gradients = 2/m *X_b.T.dot(X_b.dot(theta)-y)
theta = theta -eta *gradients
theta
'''
array([[3.75303695],
[3.08571225]])
'''theta0 = 4, theta1 = 3 과 비슷하게 찾은 것을 볼 수 있다.
- 학습률에 대한 경사하강법 변화

학습률이 너무 작을 때 (위 예시 0.02)는 수렴까지의 시간이 너무 오래걸린다는 단점이 있고, 너무 클 때는( 위 예시 0.5) 최적점을 찾지 못하고 발산하는 것을 볼 수 있다. 위와 같이 학습률이 모델의 성능에 중요한 것을 알 수 있다.
적절한 학습률을 찾으려면 어떻게 할까? 그리드 탐색을 사용해야한다. 이 때 너무 오랜 시간이 걸리므로 반복 횟수를 지정해야한다. 반복의 횟수는 벡터의 노름이 허용오차보다 작아지면 경사 하강법이 최솟값에 도달한 것이므로 중지하는 방향으로 횟수를 정해야된다.
## 확률적 경사하강법
매 스텝에서 딱 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 gradient를 계산하는 것이다
이 때 확률적(=무작위)이기 때문에 불안정하다. 따라서 반복 횟수를 높여야한다.
하지만 이러한 특성 때문에 배치 경사하강법보다 전역 최솟값을 찾을 확률이 높다. 왜냐하면 불규칙성 때문에 지역 최솟값을 건너 뛸 수 있기 때문이다.
n_epochs = 50
t0,t1 = 5,50
def learning_schedule(t):
return t0/(t+t1)
theta = np.random.randn(2,1)
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2*xi.T.dot(xi.dot(theta)-yi)
eta = learning_schedule(epoch*m+i)
theta = theta-eta*gradients
theta
'''
array([[3.7004902 ],
[3.11371943]])
'''이를 sklearn으로 구현하면 다음과 같다.
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=50,penalty=None,eta0=0.1)
sgd_reg.fit(X,y.ravel())
sgd_reg.intercept_,sgd_reg.coef_
# (array([3.75788764]), array([3.10766491]))
확률적 경사하강법은 한개의 랜덤값에 영향을 받으므로 경사하강법 보다 수렴할 때 튀는 경향이 있지만 더욱 속도가 빠르다.
## 미니 배치 경사하강법
확률적 경사하강법은 단 하나의 샘플로 수렴을 하는 방향으로 하지만 이는 이를 극복하기 위해 배치 사이즈를 조금 키워 수렴의 속도를 빠르게 하게 해준다. 이를 통해 확률적 경사하강법보다 덜 불규칙적으로 움직일 수 있게 된다. 하지만 확률적 경사하강법에 비해 지역 최솟값에서 빠져나오기 힘든 단점이 있다.

빨간색은 SGD(확률적 경사하강법)이고 매우 많이 튀는 것을 볼 수 있다.
파란색은 배치 경사하강법이고 전체 데이터셋을 통해 하기 때문에 거의 튀지 않음을 볼 수 있다. 그러나 시간이 오래 걸림이 보인다.
초록색은 미니 배치 경사하강법이고 적당히 튀고 빠른 성능을 볼 수 있다.
'핸즈온 머신러닝' 카테고리의 다른 글
| Chpater3 - 분류 (0) | 2021.01.10 |
|---|---|
| Chapter2 - 머신러닝 프로젝트 처음부터 끝까지(3) (0) | 2021.01.05 |
| Chapter2 - 머신러닝 프로젝트 처음부터 끝까지(2) (0) | 2021.01.05 |
| Chapter2 - 머신러닝 프로젝트 처음부터 끝까지(1) (1) | 2021.01.04 |
| Chapter1 - 한눈에 보는 머신러닝 (1) | 2020.12.29 |




댓글