Auto Encoding Variational Bayes(VAE) -1

원 논문

arxiv.org/abs/1312.6114

Auto-Encoding Variational Bayes

참고 자료

www.youtube.com/watch?v=KYA-GEhObIs

garden-k.medium.com/testing-b3966b642cf5

Testing

 

지금까지 읽은 논문이 몇개 안되지만 남들은 쉽다고 하는데 나한텐 너무 어려운 논문이었다... 생각보다 경제학 수업에서 배운 수학식이 나와서 그나마 감은 잡았지만...감만 잡았다..문송합니다..

이 논문은 거의 수식이 전부인 논문이라고 해도 과언이 아니다. loss 를 계산하기 위한 과정 만들어가는 것을 가장 중요시 하는 논문이라고 생각한다.

논문의 흐름대로 따라가진 않고 주요 개념들만 살펴보면서 정리해보겠다

 

## 알고있어야 하는 지식들

- Manifold hypothesis : 고차원 데이터라 할지라도, 실질적으로 해당 데이터를 나타내주는 저차원 공간인 manifold가 존재한다는 것을 의미. (ref. wiserloner.tistory.com/1137)

- AutoEncoder 

AutoEncoder

input data x를 저차원의 잠재변수(latent variables = z)로 차원 축소한 뒤, 다시 입력 데이터에 가까운 y = x' 로 복원하는 구조의 모델이다. encoder 뒤에 디코더를 붙이고 출력해야하는 정답 데이터로 입력데이터를 사용하면서 self-supervised learning이 가능해짐.

- 수학 식

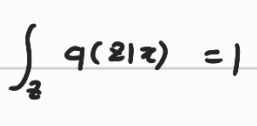
 -> 전체 확률 분포에 대해서 적분하면 1이다.

 

-> 조건부 확률

 

 - > 기대값

 

KLD

- Maximum Likelihood Estimation(MLE)

MLE 공식

어떤 확률 변수에서 샘플값들을 토대로 확률 변수의 모수를 구하는 방법

X = 어떠한 확률분포의 값(샘플 값)의 집합, θ  = 어떤 분포의 모수

ref. sanghyukchun.github.io/58/

## Variational inference

Variational inference는 어떠한 예측 확률값을 알고 싶을 때, 이와 비슷한(approximate) 확률분포를 생성하고 두 확률 분포 간의 차이를 KLD를 통해 계산하여 이를 최소화 시키는 방법이다. 이 때 비슷한 분포는 계산이 편리한 분포여야되기 때문에 가우시안 분포를 따른다.

Variational inference

p 분포는 내가 알고 싶은 확률을 말하고 q 분포는 p 분포를 근사한 approximation 분포이다. 이런 과정이 필요한 이유는 바로 계산이 불가능하기 때문이다. 사후 확률을 바로 계산하려면 p(x), p(z), p(x,z)를 알아야되지만 z 정보가 없기 때문이다.

KLD를 최소화 하기 위한 식은 다음과 같다.

equation(1)

그리고 이 식을 풀어쓰면 다음과 같다.

equation(1)을 풀어쓴 식

D_KL 이 최소화 되는 점을 찾아야 된다는 것을 풀어쓴 식으로 이해하면 된다.

첫 줄에 적분 값은 1로 좌변에 1을 곱해준 것과 같다. 그리고 이를 조건부 확률로 변환한다. 그리고 chain rule을 이용하고 log이므로 전개가 가능하므로 +를 해준다. 4번째 줄에 존재하는 빨간색 줄을 L이라고 하고(좌변과 동일) , + 이후에 있는 식을 KLD에 의해 나타내진다.

이 떄 L로 표시된 부분을 Lower bound 또는 ELBO라고 부른다. 좌변의 maximum likelihood는 항상 음수의 값을 가지고 )p(x)가 0~1), KLD는 항상 양수의 값을 가진다. 따라서 ELBO는 음수의 값이 된다. 

이에 따라 KLD 최소화 문제를 ELBO를 최대화 하는 문제로 변환할 수 있다.

 논문에서의 정리된 식은 다음과 같다.

equation(3)

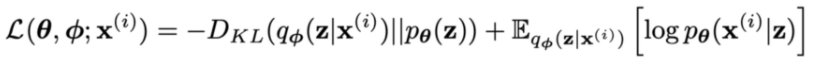
이를 유도하는 과정은 다음과 같다.

먼저 equation(2)를 보면

equation(2)

이렇게 정리되는데 이를 풀어쓰면

equation(2) 풀어쓴 식

이렇게 정리된다. 이는 기대값에 의해 정리되는데 이 식은 몬테카를로 식으로 L의 값이 계산 가능하다.

그리고 이 식을 다른 방식으로 풀면 식(3)이 유도된다.

 

equation(3) 유도식

두번째 식에서 조건부 확률로 쓰고 KLD를 도출한 다음에 equation(2) 와 같은 방법으로 기대값을 도출한다.

KLD는 수학계산이 가능하므로 variance를 줄일 수 있다. 그래서 이는 Regularization역할이 가능하다. 그리고 기대값 E는 Reconstruction error라고 불리우며 자기 자신을 얼마나 잘 복원시켰는지 측정하는 역할을 한다.

equation(2)를 몬테카를로 estimation에 적용하면 다음과 같은 식을 도출할 수 있다.

equation(2) 몬테카를로 estimation 적용

l개 만큼 샘플링한 값은 q 분포를 따르고 z들에 대해선 loss 값을 계산할 수 있다. 

equation(3)도 (2)와 같은 방식으로 풀어진다.

equation(3)에 몬테카를로 estimation 적용

## SGVB(Sochastic Gradient Variational Bayes)

SGVB

p(z)는 평균이 0인 분포를 따르고 q는 가우시안 분포를 따른다. J 는 z의 차원이다.

이는 KLD를 푸는 공식으로 알고 생각하고 넘어가면 된다.