원 논문
참고 자료
www.youtube.com/watch?v=AVvlDmhHgC4
나동빈님의 유튜브를 참고하여 진행하였는데 정말 갓동빈님이시다...설명을 이렇게 쉽게 해주시는 분은 거의 처음본다..역시 갓동빈님이시다..
위 논문은 무려 NIPS2014 에 개제된 대단한 논문이다. 사실 Image Generation 이라고 하면 GAN 알고리즘을 떠올릴 만큼 Image Generation의 대명사인 알고리즘이다.
## Abstract
기존의 생성 모델은 Markov chain이나 unrolled approximate inference network를 사용하였지만 GAN 알고리즘은 전혀 이런 과정이 필요하지 않고 오직 Neural Network만으로 구성한 알고리즘이다.
이는 generative model의 새로운 프레임 워크라고 소개한다.
여기서 D(Descriminator)와 G(Generator)의 minmax 게임이라고 표현한다. 이러한 이유는 추후에 설명하겠지만 D는 max가 목적이고 G는 min이 목적이다. 목적식을 소개할 때 자세한 설명을 진행하겠다.
## Introduction
CNN 와 같은 분류 모델은 역전파 방법으로 인해 더 deep한 Neural Network를 만들고 성능은 좋아졌지만 Generative model은 아직 확률론적인 모델들을 근사하는데에 있어서 어려움이 있었고, RELU와 같은 함수의 장점을 최대화해서 이용하기에는 어려움이 있던 상황이었다.
이러한 어려움을 극복하기 위해서 adversial nets이라는 새로운 framework를 제안한다.
이 모델은 비유하자면 위조지폐를 만드는 범죄자(Generator)와 위조지폐를 감별하는 경찰(Descriminator)의 싸움이다.
Generator와 Descriminator는 모두 multilayer perceptron으로 오직 Deep Learning으로만 학습할 수 있다. 따라서 이전까지 나왔던 다양한 Generator model 과는 큰 차별점이 있다
## Adversarial Nets
생성자와 판별자 두 개의 네트워크를 활용한 생성모델이고 생성자는 G(z), 판별자는 D(x)로 나타낸다.
이는 모두 미분 가능함을 다시금 언급한다.
그리고 다음과 같은 목적함수를 통해 생성자는 이미지 분포를 학습할 수 있다.

목적함수는 위와 같다. 위에서 언급했듯이 생성자와 판별자의 minmax 게임이다. 즉, 생성자를 minimize 하게 만드는 것이 목적이고 판별자를 maximum 하게 만드는 것이 목적인 목적함수이다.
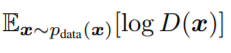
이 식을 풀어서 설명하자면 원본 데이터 분포에서 x라는 하나의 값을 sampling 하고 D에 넣는다. 그리고 이 D를 log 씌운 값의 기대값을 말한다.

이 식은 p(z)라는 noise 분포에서 랜덤한 노이즈 z를 추출하고 이를 생성자 G에 넣는다. 그리고 이 생성자(가짜 이미지)를 D에 넣는다. 그리고 1-D를 해주고 log를 씌운 값의 기댓값이다.
1-D(G(x))를 최소화 한다는 것은 Generator한 가짜 이미지가 판별자에 의해서 진짜라고 인식이 될 수 있도록 즉, 판별자가 1이 될 수 있도록 진행을 하는 것이다.
따라서 이 목적함수는 D(x)에 대해선 maximum 값인 1을 반환할 수 있도록 하고, G(x)에 대해선 minmum 값인 0을 반환할 수 있도록 학습한다. 여기서 D(x)와 G(x) 값의 범위는 0~1 사이인데 1은 real image, 0은 fake image라고 정의한다.
다시 한 번 정리하자면 원본 데이터에 있어서 1로 분류할 수 있게하고, 가짜 이미지에 대해서는 0을 뱉을 수 있도록 학습한다 라는 것이다.
실제로 학습을 할 때는 논문에서 제시한 목적함수와는 약간 다르게 log(D(G(z))를 최대화하는 방향으로 G를 학습하는 방향으로 초기 학습을 해야지 더 좋은 결과가 좋다고 주장한다.
위 식을 하나의 flow chart로 나동빈님이 정리한 것이다.

Z가 Generator를 거쳐 Fake Image를 생성하고 이 이미지는 Discriminator에 들어가서 loss를 구한 뒤에 2번째 식(G(z))이 줄어드는 방향으로 update를 하기 위해서 '-'를 붙여준다.
### GAN의 수렴과정
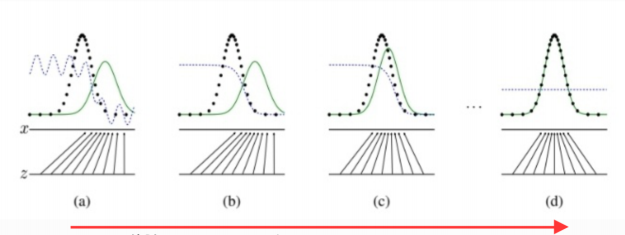
이 그림은 논문에선 교육용의 목적으로 시간의 흐름에 따라 어떻게 수렴을 하게 하는지 나타내주는 그림이다.
여기서 초록색 선은 생성모델 분포, 검은색 점 집합은 실제 이미지 분포(이산적이기 때문에 점으로 표현), 그리고 파란색 선은 판별 모델의 분포이다.
이 그림을 설명하자면 z에서 샘플링 과정을 거쳐서 생성자 x에 mapping 시키고 이를 위 목적함수를 이용하여 점점 x의 이미지와 동일하게 만드는 것이 학습의 최종 목표이다.
새로운 이미지를 뽑는 방법은 다음과 같다. 이산적으로 뽑은 검은색 점 즉, 원래 이미지 바로 옆에 연속적인 초록색 라인에서의 하나 값을 뽑으면 새로운 이미지가 생성되게 되는 것이다!
위 그림에서 파란색 선은 어느 한 값으로 수렴하게 되는데 이 값은 1/2이다. 이 값은 추후에 증명하겠지만 P_g와 P_data가 같아질 때의 값인데 이 의미는 생성자가 내보낸 이미지와 실제 이미지와 구분할 수 없다는 것을 의미한다.
### Global Optimality
Generator G가 원본 데이터 D를 학습할 수 있는 것에 대한 명제와 그에 따른 증명이다.

이 때 g는 고정됨
이를 증명하는 수학식은 다음과 같다.

편의상 첫째줄부터 1번 식이라고 칭하겠다.
1번 식은 앞서 정의하였던 목적함수이다. 여기에 밑에 식인 연속확률분포의 기대값 공식을 이용하여 2번 식으로 푼다.
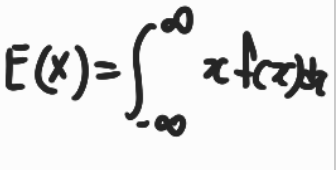
그리고 2번식에서의 z는 x와 mapping 되기 때문에 하나의 적분으로 합쳐서 3번처럼 정리한다.
3번 식의 형태는 f(y) = alog(y) + blog(1-y) 일 때 0에서 1 사이의 범위의 a/(a+b) 의 극대값을 갖는 식의 형태로 만들어 준것이다.
따라서 이를 통해 극대값 명제 D*_g(x)를 가질 수 있게 된다.
위에서 D의 극대값을 구했으니 D가 optimal한 포인트(극대값)을 가질 때의 G의 값을 구한다.
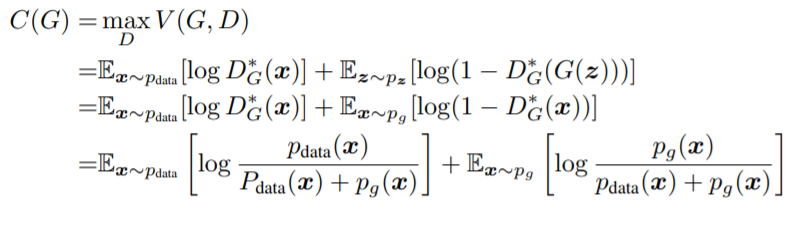
1번 목적함수에서 z는 x에 매핑되기 때문에 2번으로 바꿀 수 있고 앞서 구한 D*_G(x) 의 값을 2번에 대입하여 3번의 식을 얻을 수 있다.
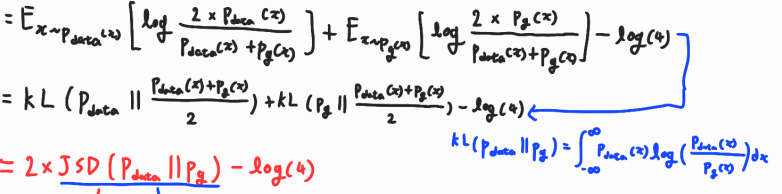
이어서 3번 식에서 계산의 편의를 위해 log 안에 2를 곱해준다. 그래서 4번식이 도출되고 -log(4)는 양 식에 2를 곱해주었기 때문에 빼준다.(로그 연산 참고)
그리고 4번에서 KLD를 사용하여 5번식과 같이 변경해준다.
그리고 5번식을 정리하여 JSD(Jenson-Shanon-Divergence) 연산의 형태로 바꿔준다.
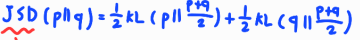
JSD로 변환해주는 이유는 distance matrix 형태로 바꿔주기 위함인데 이 식의 minimize 값은 0 이다. minimize가 되기 위한 조건은 p == q 이다. 따라서 p_g와 p_data가 같을 때 C(G)의 global minize를 구할 수 있고 이 값은 -log(4)가 된다.
즉, C(G)의 global minimum point는 P_g = P_data이고 이 때의 값은 -log(4) 이다.
따라서 Global Optima가 존재할 수 있다는 것이 증명 되었다.
### Convergence of Algorithm 1
P_g 가 G로 수렴할 수 있는지에 대한 증명이다.
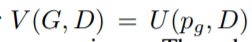
V의 함수는 앞서 증명했던 식에서 봤듯이, convex function이기 때문에 미분이 가능하다.

함수 V를 g에 대해서 미분한다면 앞에 P_data 부분은 상수처리가 되고 log(1-D(x))는 상수처리가 되어서 P_g에 있어서 V(G,D) 함수는 선형적인 함수가 되기 때문에 P_g는 G로 수렴할 수 있다.
## Experiments
Experiments 부분은 간략하게 설명하겠다. 평가 지표는 Parzen window-based log-likelihood estimate 를 사용하였고 이전의 모델들과 비교했을 때의 결과는 다음과 같다. ※ 평가지표 참고 링크 : process-mining.tistory.com/95


맨 끝 줄에 노란색 박스로 친 부분은 실제 이미지이고 나머지 부분이 GAN으로 생성된 이미지이다.
'논문 정리' 카테고리의 다른 글
| A Style Based Generator Architecture for Generative Adversarial Networks(StyleGAN) (0) | 2021.05.09 |
|---|---|
| Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks(CycleGAN) (0) | 2021.04.29 |
| Auto Encoding Variational Bayes(VAE) -1 (5) | 2021.03.29 |
| Deep Residual Learning for Image Recognition(ResNet) (4) | 2021.03.13 |
| Towards open set deep networks (4) | 2021.01.20 |




댓글